Article contents
First Passage Percolation on the Erdős–Rényi Random Graph
Published online by Cambridge University Press: 20 June 2011
Abstract
In this paper we explore first passage percolation (FPP) on the Erdős–Rényi random graph Gn(pn), where we assign independent random weights, having an exponential distribution with rate 1, to the edges. In the sparse regime, i.e., when npn → λ > 1, we find refined asymptotics both for the minimal weight of the path between uniformly chosen vertices in the giant component, as well as for the hopcount (i.e., the number of edges) on this minimal weight path. More precisely, we prove a central limit theorem for the hopcount, with asymptotic mean and variance both equal to (λ log n)/(λ − 1). Furthermore, we prove that the minimal weight centred by (log n)/(λ − 1) converges in distribution.
We also investigate the dense regime, where npn → ∞. We find that although the base graph is ultra-small (meaning that graph distances between uniformly chosen vertices are o(log n)), attaching random edge weights changes the geometry of the network completely. Indeed, the hopcount Hn satisfies the universality property that whatever the value of pn, Hn/log n → 1 in probability and, more precisely, (Hn − βn log n)/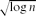 , where βn = λn/(λn − 1), has a limiting standard normal distribution. The constant βn can be replaced by 1 precisely when λn ≫
, where βn = λn/(λn − 1), has a limiting standard normal distribution. The constant βn can be replaced by 1 precisely when λn ≫ 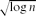 , a case that has appeared in the literature (under stronger conditions on λn) in [4, 13]. We also find lower bounds for the maximum, over all pairs of vertices, of the optimal weight and hopcount.
, a case that has appeared in the literature (under stronger conditions on λn) in [4, 13]. We also find lower bounds for the maximum, over all pairs of vertices, of the optimal weight and hopcount.
This paper continues the investigation of FPP initiated in [4] and [5]. Compared to the setting on the configuration model studied in [5], the proofs presented here are much simpler due to a direct relation between FPP on the Erdős–Rényi random graph and thinned continuous-time branching processes.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 44
- Cited by

