Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Montanari, Andrea
2015.
Finding One Community in a Sparse Graph.
Journal of Statistical Physics,
Vol. 161,
Issue. 2,
p.
273.
Meka, Raghu
Potechin, Aaron
and
Wigderson, Avi
2015.
Sum-of-squares Lower Bounds for Planted Clique.
p.
87.
Krauthgamer, Robert
Nadler, Boaz
and
Vilenchik, Dan
2015.
Do semidefinite relaxations solve sparse PCA up to the information limit?.
The Annals of Statistics,
Vol. 43,
Issue. 3,
Ames, Brendan P. W.
2015.
Guaranteed Recovery of Planted Cliques and Dense Subgraphs by Convex Relaxation.
Journal of Optimization Theory and Applications,
Vol. 167,
Issue. 2,
p.
653.
Hajek, Bruce
Wu, Yihong
and
Xu, Jiaming
2016.
Information limits for recovering a hidden community.
p.
1894.
Hajek, Bruce
Wu, Yihong
and
Xu, Jiaming
2017.
Information Limits for Recovering a Hidden Community.
IEEE Transactions on Information Theory,
Vol. 63,
Issue. 8,
p.
4729.
Montanari, Andrea
Reichman, Daniel
and
Zeitouni, Ofer
2017.
On the Limitation of Spectral Methods: From the Gaussian Hidden Clique Problem to Rank One Perturbations of Gaussian Tensors.
IEEE Transactions on Information Theory,
Vol. 63,
Issue. 3,
p.
1572.
Hajek, Bruce
Wu, Yihong
and
Xu, Jiaming
2018.
Recovering a hidden community beyond the Kesten–Stigum threshold in O(|E|log*|V|) time.
Journal of Applied Probability,
Vol. 55,
Issue. 2,
p.
325.
Hopkins, Samuel B.
Kothari, Pravesh
Potechin, Aaron Henry
Raghavendra, Prasad
and
Schramm, Tselil
2018.
On the Integrality Gap of Degree-4 Sum of Squares for Planted Clique.
ACM Transactions on Algorithms,
Vol. 14,
Issue. 3,
p.
1.
Boix-Adsera, Enric
Brennan, Matthew
and
Bresler, Guy
2019.
The Average-Case Complexity of Counting Cliques in Erdős-Rényi Hypergraphs.
p.
1256.
Leitch, Jack
Alexander, Kathleen A.
and
Sengupta, Srijan
2019.
Toward epidemic thresholds on temporal networks: a review and open questions.
Applied Network Science,
Vol. 4,
Issue. 1,
Chen, Lijie
and
Grossman, Ofer
2019.
Broadcast Congested Clique.
p.
248.
Rácz, Miklós Z.
and
Schiffer, Benjamin
2020.
Finding a planted clique by adaptive probing
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 17,
Issue. 2,
p.
775.
Bogerd, Kay
Castro, Rui M.
and
van der Hofstad, Remco
2020.
Cliques in rank-1 random graphs: The role of inhomogeneity.
Bernoulli,
Vol. 26,
Issue. 1,
Bombina, Polina
and
Ames, Brendan
2020.
Convex Optimization for the Densest Subgraph and Densest Submatrix Problems.
SN Operations Research Forum,
Vol. 1,
Issue. 3,
Hillar, Christopher
Chan, Tenzin
Taubman, Rachel
and
Rolnick, David
2021.
Hidden Hypergraphs, Error-Correcting Codes, and Critical Learning in Hopfield Networks.
Entropy,
Vol. 23,
Issue. 11,
p.
1494.
Wu, Yihong
and
Xu, Jiaming
2021.
Information-Theoretic Methods in Data Science.
p.
383.
Luo, Yuetian
and
Zhang, Anru R.
2022.
Tensor clustering with planted structures: Statistical optimality and computational limits.
The Annals of Statistics,
Vol. 50,
Issue. 1,
Huleihel, Wasim
2022.
Inferring Hidden Structures in Random Graphs.
IEEE Transactions on Signal and Information Processing over Networks,
Vol. 8,
Issue. ,
p.
855.
Marino, Raffaele
and
Kirkpatrick, Scott
2023.
Hard optimization problems have soft edges.
Scientific Reports,
Vol. 13,
Issue. 1,
 $\frac12$. This random graph model is denoted
$\frac12$. This random graph model is denoted 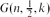 $G(n,\frac12,k)$. The hidden clique problem is to design an algorithm that finds the k-clique in polynomial time with high probability. An algorithm due to Alon, Krivelevich and Sudakov [3] uses spectral techniques to find the hidden clique with high probability when
$G(n,\frac12,k)$. The hidden clique problem is to design an algorithm that finds the k-clique in polynomial time with high probability. An algorithm due to Alon, Krivelevich and Sudakov [3] uses spectral techniques to find the hidden clique with high probability when 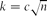 $k = c \sqrt{n}$ for a sufficiently large constant c > 0. Recently, an algorithm that solves the same problem was proposed by Feige and Ron [12]. It has the advantages of being simpler and more intuitive, and of an improved running time of O(n2). However, the analysis in [12] gives a success probability of only 2/3. In this paper we present a new algorithm for finding hidden cliques that both runs in time O(n2) (that is, linear in the size of the input) and has a failure probability that tends to 0 as n tends to ∞. We develop this algorithm in the more general setting where the clique is replaced by a dense random graph.
$k = c \sqrt{n}$ for a sufficiently large constant c > 0. Recently, an algorithm that solves the same problem was proposed by Feige and Ron [12]. It has the advantages of being simpler and more intuitive, and of an improved running time of O(n2). However, the analysis in [12] gives a success probability of only 2/3. In this paper we present a new algorithm for finding hidden cliques that both runs in time O(n2) (that is, linear in the size of the input) and has a failure probability that tends to 0 as n tends to ∞. We develop this algorithm in the more general setting where the clique is replaced by a dense random graph.
