Article contents
Expanders Are Universal for the Class of All Spanning Trees
Published online by Cambridge University Press: 03 January 2013
Abstract
A graph is called universal for a given graph class 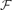 (or, equivalently,
(or, equivalently, 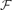 -universal) if it contains a copy of every graph in
-universal) if it contains a copy of every graph in 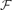 as a subgraph. The construction of sparse universal graphs for various classes
as a subgraph. The construction of sparse universal graphs for various classes 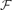 has received a considerable amount of attention. There is particular interest in tight
has received a considerable amount of attention. There is particular interest in tight 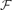 -universal graphs, that is, graphs whose number of vertices is equal to the largest number of vertices in a graph from
-universal graphs, that is, graphs whose number of vertices is equal to the largest number of vertices in a graph from 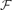 . Arguably, the most studied case is that when
. Arguably, the most studied case is that when 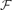 is some class of trees. In this work, we are interested in
is some class of trees. In this work, we are interested in  (n,Δ), the class of all n-vertex trees with maximum degree at most Δ. We show that every n-vertex graph satisfying certain natural expansion properties is
(n,Δ), the class of all n-vertex trees with maximum degree at most Δ. We show that every n-vertex graph satisfying certain natural expansion properties is  (n,Δ)-universal. Our methods also apply to the case when Δ is some function of n. Since random graphs are known to be good expanders, our result implies, in particular, that there exists a positive constant c such that the random graph G(n,cn−1/3log2n) is asymptotically almost surely (a.a.s.) universal for
(n,Δ)-universal. Our methods also apply to the case when Δ is some function of n. Since random graphs are known to be good expanders, our result implies, in particular, that there exists a positive constant c such that the random graph G(n,cn−1/3log2n) is asymptotically almost surely (a.a.s.) universal for  (n,O(1)). Moreover, a corresponding result holds for the random regular graph of degree cn2/3log2n. Another interesting consequence is the existence of locally sparse n-vertex
(n,O(1)). Moreover, a corresponding result holds for the random regular graph of degree cn2/3log2n. Another interesting consequence is the existence of locally sparse n-vertex  (n,Δ)-universal graphs. For example, we show that one can (randomly) construct n-vertex
(n,Δ)-universal graphs. For example, we show that one can (randomly) construct n-vertex  (n,O(1))-universal graphs with clique number at most five. This complements the construction of Bhatt, Chung, Leighton and Rosenberg (1989), whose
(n,O(1))-universal graphs with clique number at most five. This complements the construction of Bhatt, Chung, Leighton and Rosenberg (1989), whose  (n,Δ)-universal graphs with merely O(n) edges contain large cliques of size Ω(Δ). Finally, we show that random graphs are robustly
(n,Δ)-universal graphs with merely O(n) edges contain large cliques of size Ω(Δ). Finally, we show that random graphs are robustly  (n,Δ)-universal in the context of the Maker–Breaker tree-universality game.
(n,Δ)-universal in the context of the Maker–Breaker tree-universality game.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2013
References
- 9
- Cited by

