Article contents
Covering Complete r-Graphs with Spanning Complete r-Partite r-Graphs
Published online by Cambridge University Press: 09 February 2011
Abstract
An r-cut of the complete r-uniform hypergraph Krn is obtained by partitioning its vertex set into r parts and taking all edges that meet every part in exactly one vertex. In other words it is the edge set of a spanning complete r-partite subhypergraph of Krn. An r-cut cover is a collection of r-cuts such that each edge of Krn is in at least one of the cuts. While in the graph case r = 2 any 2-cut cover on average covers each edge at least 2-o(1) times, when r is odd we exhibit an r-cut cover in which each edge is covered exactly once. When r is even no such decomposition can exist, but we can bound the average number of times an edge is cut in an r-cut cover between 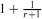 and
and 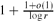 . The upper bound construction can be reformulated in terms of a natural polyhedral problem or as a probability problem, and we solve the latter asymptotically.
. The upper bound construction can be reformulated in terms of a natural polyhedral problem or as a probability problem, and we solve the latter asymptotically.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 3
- Cited by

