Article contents
The Asymptotic Number of Connected d-Uniform Hypergraphs†
Published online by Cambridge University Press: 13 February 2014
Abstract
For d ≥ 2, let Hd(n,p) denote a random d-uniform hypergraph with n vertices in which each of the 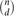 $\binom{n}{d}$ possible edges is present with probability p=p(n) independently, and let Hd(n,m) denote a uniformly distributed d-uniform hypergraph with n vertices and m edges. Let either H=Hd(n,m) or H=Hd(n,p), where m/n and
$\binom{n}{d}$ possible edges is present with probability p=p(n) independently, and let Hd(n,m) denote a uniformly distributed d-uniform hypergraph with n vertices and m edges. Let either H=Hd(n,m) or H=Hd(n,p), where m/n and 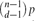 $\binom{n-1}{d-1}p$ need to be bounded away from (d−1)−1 and 0 respectively. We determine the asymptotic probability that H is connected. This yields the asymptotic number of connected d-uniform hypergraphs with given numbers of vertices and edges. We also derive a local limit theorem for the number of edges in Hd(n,p), conditioned on Hd(n,p) being connected.
$\binom{n-1}{d-1}p$ need to be bounded away from (d−1)−1 and 0 respectively. We determine the asymptotic probability that H is connected. This yields the asymptotic number of connected d-uniform hypergraphs with given numbers of vertices and edges. We also derive a local limit theorem for the number of edges in Hd(n,p), conditioned on Hd(n,p) being connected.
Keywords
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2014
Footnotes
An extended abstract version of this work appeared in the proceedings of RANDOM 2007, Vol. 4627 of Lecture Notes in Computer Science, Springer, pp. 341–352.
References
A correction has been issued for this article:
- 6
- Cited by
Linked content
Please note a has been issued for this article.

