No CrossRef data available.
Article contents
Asymmetric Rényi Problem
Published online by Cambridge University Press: 27 June 2018
Abstract
In 1960 Rényi, in his Michigan State University lectures, asked for the number of random queries necessary to recover a hidden bijective labelling of n distinct objects. In each query one selects a random subset of labels and asks, which objects have these labels? We consider here an asymmetric version of the problem in which in every query an object is chosen with probability p > 1/2 and we ignore ‘inconclusive’ queries. We study the number of queries needed to recover the labelling in its entirety (Hn), before at least one element is recovered (Fn), and to recover a randomly chosen element (Dn). This problem exhibits several remarkable behaviours: Dn converges in probability but not almost surely; Hn and Fn exhibit phase transitions with respect to p in the second term. We prove that for p > 1/2 with high probability we need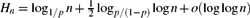 $$H_n=\log_{1/p} n +{\tfrac{1}{2}} \log_{p/(1-p)}\log n +o(\log \log n)$$
$$H_n=\log_{1/p} n +{\tfrac{1}{2}} \log_{p/(1-p)}\log n +o(\log \log n)$$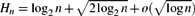 $$ H_n=\log_{2} n +\sqrt{2 \log_{2} n} +o(\sqrt{\log n})$$
$$ H_n=\log_{2} n +\sqrt{2 \log_{2} n} +o(\sqrt{\log n})$$
MSC classification
Information
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 28 , Special Issue 4: Analysis of Algorithms , July 2019 , pp. 542 - 573
- Copyright
- Copyright © Cambridge University Press 2018
Footnotes
Research partially supported by Austrian Science Foundation FWF grant F50-02.
Research supported by NSF Center for Science of Information (CSoI) grant CCF-0939370.
Research partially supported by NSF Center for Science of Information (CSoI) grant CCF-0939370, and in addition by NSF grants CCF-1524312, and NIH grant 1U01CA198941-01.

