Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Glebov, Roman
Králʼ, Daniel
and
Volec, Jan
2013.
An application of flag algebras to a problem of Erdős and Sós.
Electronic Notes in Discrete Mathematics,
Vol. 43,
Issue. ,
p.
171.
Razborov, Alexander A.
2013.
The Mathematics of Paul Erdős II.
p.
207.
PIKHURKO, OLEG
and
VAUGHAN, EMIL R.
2013.
Minimum Number ofk-Cliques in Graphs with Bounded Independence Number.
Combinatorics, Probability and Computing,
Vol. 22,
Issue. 6,
p.
910.
Разборов, Александр Александрович
and
Razborov, Alexander Alexandrovich
2014.
О $(3,4)$-проблеме Турана с запрещенными подграфами.
Математические заметки,
Vol. 95,
Issue. 2,
p.
271.
Razborov, A. A.
2014.
On Turán’s (3,4)-problem with forbidden subgraphs.
Mathematical Notes,
Vol. 95,
Issue. 1-2,
p.
245.
Pikhurko, Oleg
2014.
ON possible Turán densities.
Israel Journal of Mathematics,
Vol. 201,
Issue. 1,
p.
415.
Baber, Rahil
and
Talbot, John
2014.
A Solution to the 2/3 Conjecture.
SIAM Journal on Discrete Mathematics,
Vol. 28,
Issue. 2,
p.
756.
BALOGH, JÓZSEF
HU, PING
LIDICKÝ, BERNARD
PIKHURKO, OLEG
UDVARI, BALÁZS
and
VOLEC, JAN
2015.
Minimum Number of Monotone Subsequences of Length 4 in Permutations.
Combinatorics, Probability and Computing,
Vol. 24,
Issue. 4,
p.
658.
Falgas--Ravry, Victor
Marchant, Edward
Pikhurko, Oleg
and
Vaughan, Emil R.
2015.
The Codegree Threshold for 3-Graphs with Independent Neighborhoods.
SIAM Journal on Discrete Mathematics,
Vol. 29,
Issue. 3,
p.
1504.
Even-Zohar, Chaim
and
Linial, Nati
2015.
A Note on the Inducibility of $$4$$ 4 -Vertex Graphs.
Graphs and Combinatorics,
Vol. 31,
Issue. 5,
p.
1367.
Alon, Noga
Naves, Humberto
and
Sudakov, Benny
2016.
On the Maximum Quartet Distance between Phylogenetic Trees.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 2,
p.
718.
HEFETZ, DAN
and
TYOMKYN, MYKHAYLO
2016.
Universality of Graphs with Few Triangles and Anti-Triangles.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 4,
p.
560.
Grosu, Codruţ
2016.
On the algebraic and topological structure of the set of Turán densities.
Journal of Combinatorial Theory, Series B,
Vol. 118,
Issue. ,
p.
137.
Glebov, Roman
Král’, Daniel
and
Volec, Jan
2016.
A problem of Erdős and Sós on 3-graphs.
Israel Journal of Mathematics,
Vol. 211,
Issue. 1,
p.
349.
Falgas-Ravry, Victor
Pikhurko, Oleg
Vaughan, Emil
and
Volec, Jan
2017.
The codegree threshold ofK4−.
Electronic Notes in Discrete Mathematics,
Vol. 61,
Issue. ,
p.
407.
Gethner, Ellen
Hogben, Leslie
Lidický, Bernard
Pfender, Florian
Ruiz, Amanda
and
Young, Michael
2017.
On Crossing Numbers of Complete Tripartite and Balanced Complete Multipartite Graphs.
Journal of Graph Theory,
Vol. 84,
Issue. 4,
p.
552.
Nagami Coregliano, Leonardo
2018.
Quasi‐carousel tournaments.
Journal of Graph Theory,
Vol. 88,
Issue. 1,
p.
192.
Raymond, Annie
Singh, Mohit
and
Thomas, Rekha R.
2018.
Symmetry in Turán sums of squares polynomials from flag algebras.
Algebraic Combinatorics,
Vol. 1,
Issue. 2,
p.
249.
Raymond, Annie
Saunderson, James
Singh, Mohit
and
Thomas, Rekha R.
2018.
Symmetric sums of squares over k-subset hypercubes.
Mathematical Programming,
Vol. 167,
Issue. 2,
p.
315.
Grzesik, Andrzej
Hu, Ping
and
Volec, Jan
2019.
Minimum number of edges that occur in odd cycles.
Journal of Combinatorial Theory, Series B,
Vol. 137,
Issue. ,
p.
65.
 \begin{align*}\pi (K_4^-, C_5, F_{3,2})=12/49, \pi (K_4^-, F_{3,2})=5/18 \textrm {and} \pi (J_4, F_{3,2})=\pi (J_5, F_{3,2})=3/8,\end{align*}
\begin{align*}\pi (K_4^-, C_5, F_{3,2})=12/49, \pi (K_4^-, F_{3,2})=5/18 \textrm {and} \pi (J_4, F_{3,2})=\pi (J_5, F_{3,2})=3/8,\end{align*} $\binom{|A|}{2}$ 3-edges containing x. We also prove two Turán density results where we forbid certain induced subgraphs:
$\binom{|A|}{2}$ 3-edges containing x. We also prove two Turán density results where we forbid certain induced subgraphs: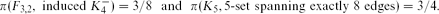 \begin{align*}\pi (F_{3,2}, \textrm { induced }K_4^-)=3/8 \textrm {and} \pi (K_5, 5\textrm {-set spanning exactly 8 edges})=3/4.\end{align*}
\begin{align*}\pi (F_{3,2}, \textrm { induced }K_4^-)=3/8 \textrm {and} \pi (K_5, 5\textrm {-set spanning exactly 8 edges})=3/4.\end{align*} \begin{align*}\pi (K_4, 4\textrm {-set spanning exactly 1 edge})=5/9.\end{align*}
\begin{align*}\pi (K_4, 4\textrm {-set spanning exactly 1 edge})=5/9.\end{align*}
