Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rok, Alexandre
and
Walczak, Bartosz
2014.
Outerstring graphs are χ-bounded.
p.
136.
Matoušek, Jiří
2014.
Geometry, Structure and Randomness in Combinatorics.
p.
61.
MATOUŠEK, JIŘÍ
2014.
Near-Optimal Separators in String Graphs.
Combinatorics, Probability and Computing,
Vol. 23,
Issue. 1,
p.
135.
Krawczyk, Tomasz
and
Walczak, Bartosz
2014.
Automata, Languages, and Programming.
Vol. 8572,
Issue. ,
p.
738.
Conlon, David
Fox, Jacob
and
Sudakov, Benny
2015.
Surveys in Combinatorics 2015.
p.
49.
Krawczyk, Tomasz
Pawlik, Arkadiusz
and
Walczak, Bartosz
2015.
Coloring Triangle-Free Rectangle Overlap Graphs with $$O(\log \log n)$$ O ( log log n ) Colors.
Discrete & Computational Geometry,
Vol. 53,
Issue. 1,
p.
199.
Mustafa, Nabil H.
and
Pach, János
2015.
Graph Drawing and Network Visualization.
Vol. 9411,
Issue. ,
p.
207.
Suk, Andrew
and
Walczak, Bartosz
2015.
New bounds on the maximum number of edges in k-quasi-planar graphs.
Computational Geometry,
Vol. 50,
Issue. ,
p.
24.
Ackerman, Eyal
Keszegh, Balázs
and
Vizer, Mate
2016.
Graph Drawing and Network Visualization.
Vol. 9801,
Issue. ,
p.
311.
PACH, JÁNOS
and
WALCZAK, BARTOSZ
2016.
Decomposition of Multiple Packings with Subquadratic Union Complexity.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 1,
p.
145.
Mustafa, Nabil H.
and
Pach, János
2016.
On the Zarankiewicz problem for intersection hypergraphs.
Journal of Combinatorial Theory, Series A,
Vol. 141,
Issue. ,
p.
1.
Janson, Svante
and
Uzzell, Andrew J.
2017.
On String Graph Limits and the Structure of a Typical String Graph.
Journal of Graph Theory,
Vol. 84,
Issue. 4,
p.
386.
Krawczyk, Tomasz
and
Walczak, Bartosz
2017.
On-Line Approach to Off-Line Coloring Problems on Graphs with Geometric Representations.
Combinatorica,
Vol. 37,
Issue. 6,
p.
1139.
Dujmović, Vida
Joret, Gwenaël
Morin, Pat
Norin, Sergey
and
Wood, David R.
2018.
Orthogonal Tree Decompositions of Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 2,
p.
839.
Do, Thao T.
2018.
Zarankiewicz's problem for semi-algebraic hypergraphs.
Journal of Combinatorial Theory, Series A,
Vol. 158,
Issue. ,
p.
621.
Bonnet, Édouard
and
Rzążewski, Paweł
2019.
Optimality Program in Segment and String Graphs.
Algorithmica,
Vol. 81,
Issue. 7,
p.
3047.
Rok, Alexandre
and
Walczak, Bartosz
2019.
Outerstring Graphs are $\chi$-Bounded.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 4,
p.
2181.
Rok, Alexandre
and
Walczak, Bartosz
2019.
Coloring Curves that Cross a Fixed Curve.
Discrete & Computational Geometry,
Vol. 61,
Issue. 4,
p.
830.
Dujmovic, Vida
Joret, Gwenaël
Micek, Piotr
Morin, Pat
Ueckerdt, Torsten
and
Wood, David
2019.
Planar Graphs have Bounded Queue-Number.
p.
862.
Dujmović, Vida
Joret, Gwenaël
Micek, Piotr
Morin, Pat
Ueckerdt, Torsten
and
Wood, David R.
2020.
Planar Graphs Have Bounded Queue-Number.
Journal of the ACM,
Vol. 67,
Issue. 4,
p.
1.
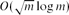 $O(\sqrt{m}\log m)$. In the present note, this bound is combined with a result of the authors, according to which every dense string graph contains a large complete balanced bipartite graph. Three applications are given concerning string graphs G with n vertices: (i) if Kt ⊈ G for some t, then the chromatic number of G is at most (log n)O(log t); (ii) if Kt,t ⊈ G, then G has at most t(log t)O(1)n edges,; and (iii) a lopsided Ramsey-type result, which shows that the Erdős–Hajnal conjecture almost holds for string graphs.
$O(\sqrt{m}\log m)$. In the present note, this bound is combined with a result of the authors, according to which every dense string graph contains a large complete balanced bipartite graph. Three applications are given concerning string graphs G with n vertices: (i) if Kt ⊈ G for some t, then the chromatic number of G is at most (log n)O(log t); (ii) if Kt,t ⊈ G, then G has at most t(log t)O(1)n edges,; and (iii) a lopsided Ramsey-type result, which shows that the Erdős–Hajnal conjecture almost holds for string graphs.
