Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
TREGLOWN, ANDREW
2015.
On Directed Versions of the Hajnal–Szemerédi Theorem.
Combinatorics, Probability and Computing,
Vol. 24,
Issue. 6,
p.
873.
Balogh, József
Molla, Theodore
and
Sharifzadeh, Maryam
2016.
Triangle factors of graphs without large independent sets and of weighted graphs.
Random Structures & Algorithms,
Vol. 49,
Issue. 4,
p.
669.
Treglown, Andrew
2016.
A degree sequence Hajnal–Szemerédi theorem.
Journal of Combinatorial Theory, Series B,
Vol. 118,
Issue. ,
p.
13.
Balogh, József
Lo, Allan
and
Molla, Theodore
2017.
Transitive triangle tilings in oriented graphs.
Journal of Combinatorial Theory, Series B,
Vol. 124,
Issue. ,
p.
64.
Kierstead, H. A.
Kostochka, A. V.
and
McConvey, A.
2017.
Strengthening Theorems of Dirac and Erdős on Disjoint Cycles.
Journal of Graph Theory,
Vol. 85,
Issue. 4,
p.
788.
CZYGRINOW, ANDRZEJ
DEBIASIO, LOUIS
MOLLA, THEODORE
and
TREGLOWN, ANDREW
2018.
TILING DIRECTED GRAPHS WITH TOURNAMENTS.
Forum of Mathematics, Sigma,
Vol. 6,
Issue. ,
Simonovits, Miklós
and
Szemerédi, Endre
2019.
Building Bridges II.
Vol. 28,
Issue. ,
p.
445.
Han, Jie
Morris, Patrick
and
Treglown, Andrew
2021.
Tilings in randomly perturbed graphs: Bridging the gap between Hajnal‐Szemerédi and Johansson‐Kahn‐Vu.
Random Structures & Algorithms,
Vol. 58,
Issue. 3,
p.
480.
DeBiasio, Louis
Lo, Allan
Molla, Theodore
and
Treglown, Andrew
2021.
Transitive Tournament Tilings in Oriented Graphs with Large Minimum Total Degree.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 1,
p.
250.
Balogh, József
Csaba, Béla
Pluhár, András
and
Treglown, Andrew
2021.
A discrepancy version of the Hajnal–Szemerédi theorem.
Combinatorics, Probability and Computing,
Vol. 30,
Issue. 3,
p.
444.
Cheng, Yangyang
Han, Jie
Wang, Bin
and
Wang, Guanghui
2023.
Rainbow spanning structures in graph and hypergraph systems.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Lih, Ko-Wei
2025.
Handbook of Combinatorial Optimization.
p.
1.
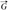 $\vv G$ with |
$\vv G$ with | 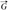 $\vv G$ | = ks and δ(
$\vv G$ | = ks and δ( 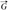 $\vv G$ ) ⩾ 2k(s − 1) − 1 contains k disjoint transitive tournaments on s vertices, where δ(
$\vv G$ ) ⩾ 2k(s − 1) − 1 contains k disjoint transitive tournaments on s vertices, where δ( 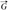 $\vv G$ )= minv∈V (
$\vv G$ )= minv∈V ( 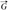 $\vv G$ )d −(v)+d +(v). Our result implies the Hajnal–Szemerédi theorem, and its degree bound is optimal. We also make some conjectures regarding even more general results for multigraphs and partitioning into other tournaments. One of these conjectures is supported by an asymptotic result.
$\vv G$ )d −(v)+d +(v). Our result implies the Hajnal–Szemerédi theorem, and its degree bound is optimal. We also make some conjectures regarding even more general results for multigraphs and partitioning into other tournaments. One of these conjectures is supported by an asymptotic result.
