No CrossRef data available.
Article contents
Additive bases via Fourier analysis
Published online by Cambridge University Press: 29 April 2021
Abstract
Extending a result by Alon, Linial, and Meshulam to abelian groups, we prove that if G is a finite abelian group of exponent m and S is a sequence of elements of G such that any subsequence of S consisting of at least 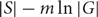 $$|S| - m\ln |G|$$ elements generates G, then S is an additive basis of G . We also prove that the additive span of any l generating sets of G contains a coset of a subgroup of size at least
$$|S| - m\ln |G|$$ elements generates G, then S is an additive basis of G . We also prove that the additive span of any l generating sets of G contains a coset of a subgroup of size at least 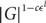 $$|G{|^{1 - c{ \in ^l}}}$$ for certain c=c(m) and
$$|G{|^{1 - c{ \in ^l}}}$$ for certain c=c(m) and 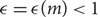 $$ \in=\in (m) < 1$$; we use the probabilistic method to give sharper values of c(m) and
$$ \in=\in (m) < 1$$; we use the probabilistic method to give sharper values of c(m) and 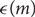 $$ \in (m)$$ in the case when G is a vector space; and we give new proofs of related known results.
$$ \in (m)$$ in the case when G is a vector space; and we give new proofs of related known results.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Alon, N., Linial, N. and Meshulam, R. (1991) Additive bases of vector spaces over prime fields. J. Comb. Theory Ser. A. 57 203–210.CrossRefGoogle Scholar
Hatami, H. and de Quehen, V. (2016) On the additive bases problem in finite fields. Electron. J. Comb. 23(3) P3.33.Google Scholar
Jaeger, F., Linial, N., Payan, C. and Tarsi, M. (1992) Group connectivity of graphs—A nonhomogeneous analogue of nowhere-zero flow properties. J. Comb. Theory Ser. B 56 165–182.CrossRefGoogle Scholar
Lev, V. F., Muzychuk, M. E. and Pinchasi, R. (2010) Additive bases in abelian groups, Int. J. Number Theory 6(4) 799–809.CrossRefGoogle Scholar
Tao, T. (2005) An uncertainty principle for cyclic groups of prime order. Math. Res. Lett. 12(1) 121–127.CrossRefGoogle Scholar


