Article contents
Probably Intersecting Families are Not Nested
Published online by Cambridge University Press: 09 October 2012
Abstract
It is well known that an intersecting family of subsets of an n-element set can contain at most 2n−1 sets. It is natural to wonder how ‘close’ to intersecting a family of size greater than 2n−1 can be. Katona, Katona and Katona introduced the idea of a ‘most probably intersecting family’. Suppose that 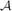 is a family and that 0 < p < 1. Let
is a family and that 0 < p < 1. Let 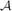 (p) be the (random) family formed by selecting each set in
(p) be the (random) family formed by selecting each set in 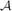 independently with probability p. A family
independently with probability p. A family 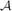 is most probably intersecting if it maximizes the probability that
is most probably intersecting if it maximizes the probability that 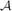 (p) is intersecting over all families of size |
(p) is intersecting over all families of size |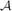 |.
|.
Katona, Katona and Katona conjectured that there is a nested sequence consisting of most probably intersecting families of every possible size. We show that this conjecture is false for every value of p provided that n is sufficiently large.
Keywords
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 2
- Cited by

