Article contents
Line-of-Sight Percolation
Published online by Cambridge University Press: 01 March 2009
Abstract
Given ω ≥ 1, let  be the graph with vertex set
be the graph with vertex set 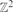 in which two vertices are joined if they agree in one coordinate and differ by at most ω in the other. (Thus
in which two vertices are joined if they agree in one coordinate and differ by at most ω in the other. (Thus 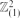 is precisely
is precisely 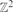 .) Let pc(ω) be the critical probability for site percolation on
.) Let pc(ω) be the critical probability for site percolation on  . Extending recent results of Frieze, Kleinberg, Ravi and Debany, we show that limω→∞ωpc(ω)=log(3/2). We also prove analogues of this result for the n-by-n grid and in higher dimensions, the latter involving interesting connections to Gilbert's continuum percolation model. To prove our results, we explore the component of the origin in a certain non-standard way, and show that this exploration is well approximated by a certain branching random walk.
. Extending recent results of Frieze, Kleinberg, Ravi and Debany, we show that limω→∞ωpc(ω)=log(3/2). We also prove analogues of this result for the n-by-n grid and in higher dimensions, the latter involving interesting connections to Gilbert's continuum percolation model. To prove our results, we explore the component of the origin in a certain non-standard way, and show that this exploration is well approximated by a certain branching random walk.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
- 11
- Cited by

