Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boyd, David W.
1980.
Speculations Concerning the Range of Mahler's Measure.
Canadian Mathematical Bulletin,
Vol. 24,
Issue. 4,
p.
453.
Boyd, David W.
1980.
Reciprocal polynomials having small measure.
Mathematics of Computation,
Vol. 35,
Issue. 152,
p.
1361.
Smyth, C. J.
1980.
On the measure of totally real algebraic integers.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 30,
Issue. 2,
p.
137.
Myerson, Gerald
1984.
A Measure for Polynomials in Several Variables.
Canadian Mathematical Bulletin,
Vol. 27,
Issue. 2,
p.
185.
Rhin, Georges
and
Smyth, Christopher
1995.
On the absolute Mahler measure of polynomials having all zeros in a sector.
Mathematics of Computation,
Vol. 64,
Issue. 209,
p.
295.
Doche, Christophe
2000.
On the spectrum of the Zhang-Zagier height.
Mathematics of Computation,
Vol. 70,
Issue. 233,
p.
419.
Borwein, Peter
2002.
Computational Excursions in Analysis and Number Theory.
p.
15.
Pritsker, Igor E.
2008.
An areal analog of Mahler’s measure.
Illinois Journal of Mathematics,
Vol. 52,
Issue. 2,
Huang, Hansong
2011.
Mahler’s measures on function spaces.
Illinois Journal of Mathematics,
Vol. 55,
Issue. 3,
Mu, Quanwu
and
Wu, Qiang
2013.
The measure of totally positive algebraic integers.
Journal of Number Theory,
Vol. 133,
Issue. 1,
p.
12.
Wu, Qiang
and
Tian, Xiaoxia
2014.
THE ABSOLUTE LENGTH OF ALGEBRAIC INTEGERS WITH POSITIVE REAL PARTS.
Taiwanese Journal of Mathematics,
Vol. 18,
Issue. 1,
Verger-Gaugry, Jean-Louis
2016.
On the Conjecture of Lehmer, Limit Mahler Measure of Trinomials and Asymptotic Expansions.
Uniform distribution theory,
Vol. 11,
Issue. 1,
p.
79.
Myerson, G
2017.
Number Theory with an Emphasis on the Markoff Spectrum.
p.
163.

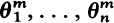 The condition on the size of the roots and the fact that the
The condition on the size of the roots and the fact that the 