Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-29T01:54:08.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary Perfect Numbers

Published online by Cambridge University Press:  20 November 2018

M.V. Subbarao  and
L. J. Warren
M.V. Subbarao
Affiliation:
University of Alberta, Edmonton and San Diego State College
L. J. Warren
Affiliation:
University of Alberta, Edmonton and San Diego State College
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let σ*(N) denote the sum of the unitary divisors of N, that is,

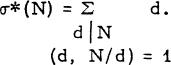
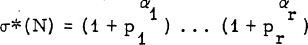It is easily seen that σ*(N) is multiplicative. In fact σ*(l) = 1 if N > 1 has the prime decomposition 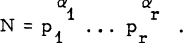. Let us define a positive integer to be unitary perfect whenever σ*(N) = 2N. The first four such numbers are 6, 60, 90 and 87, 360. In a recent abstract [ l ] published by one of us, the last of these numbers was overlooked. No other unitary perfect numbers are known to the authors.

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 2 , June 1966 , pp. 147 - 153
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Subbarao, M.V., On unitary perfect numbers, Notices Amer. Math. Soc. 12, No. 3 (1965), p. 368.Google Scholar