Article contents
Unisolvence on Multidimensional Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
In this note we consider the possibility of unisolvence of a family 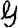 of real continuous functions on a compact subset X of m-dimensional Euclidean space. Such a study is of interest for two reasons. First, an elegant theory of Chebyshev approximation has been constructed for the case where the approximating family
of real continuous functions on a compact subset X of m-dimensional Euclidean space. Such a study is of interest for two reasons. First, an elegant theory of Chebyshev approximation has been constructed for the case where the approximating family 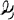 is unisolvent of degree n on an interval [α, β]. We study what sort of theory results from unisolvence of degree n on a more general space. Secondly, uniqueness of best Chebyshev approximation on a general compact space to any continuous function on X can be shown if the approximating family
is unisolvent of degree n on an interval [α, β]. We study what sort of theory results from unisolvence of degree n on a more general space. Secondly, uniqueness of best Chebyshev approximation on a general compact space to any continuous function on X can be shown if the approximating family 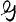 is unisolvent of degree n and
is unisolvent of degree n and 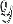 satisfies certain convexity conditions. It is therefore of importance to Chebyshev approximation to consider the domains X on which unisolvence can occur. We will also study a more general condition on
satisfies certain convexity conditions. It is therefore of importance to Chebyshev approximation to consider the domains X on which unisolvence can occur. We will also study a more general condition on 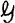 involving a variable degree.
involving a variable degree.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1968
References
- 3
- Cited by

