If 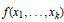$f({{x}_{1}},...,{{x}_{k}})$ is a polynomial with complex coefficients, the Mahler measure o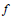f $f$ , 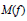$M(f)$ is defined to be the geometric mean of 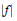$|f|$ over the $k$ -torus 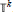${{\mathbb{T}}^{k}}$ . We construct a sequence of approximations 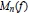${{M}_{n}}\,(f)$ which satisfy 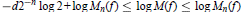$-d{{2}^{-n}}\,\log \,2\,+\,\log \,{{M}_{n}}(f)\,\le \,\log \,M(f)\,\le \,\log \,{{M}_{n}}(f)$ . We use these to prove that 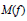$M(f)$ is a continuous function of the coefficients of 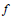$f$ for polynomials of fixed total degree 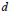$d$ . Since 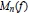${{M}_{n}}\,(f)$ can be computed in a finite number of arithmetic operations from the coefficients of 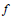$f$ this also demonstrates an effective (but impractical) method for computing 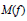$M(f)$ to arbitrary accuracy.