Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T05:47:29.513Z Has data issue: false hasContentIssue false
  • English
  • Français

Un nouveau point de repère dans la théorie des formes automorphes

Published online by Cambridge University Press:  20 November 2018

Robert P. Langlands
Robert P. Langlands*
Affiliation:
Institute for Advanced Study, School of Mathematics, 1 Einstein Drive, Princeton, NJ 08540, U.S.A. email: rpl@ias.edu
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Ceux qui connaissent l’auteur et ses écrits, comme par exemple 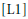$\left[ \text{L1} \right]$ et 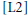$\left[ \text{L2} \right]$, savent que la notion de fonctorialité et les conjectures rattachées à celle-ci ont été introduites —en suivant ce que Artin avait fait pour un ensemble plus restreint de fonctions— pour aborder le problème de la prolongation analytique générale des fonctions 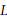$L$-automorphes. Ils savent en plus que je suis d’avis que seules les méthodes basées sur la formule des traces pourront aller au fond des problèmes. Il n’en reste pas moins que malgré de récents progrès importants sur le lemme fondamental et la formule des traces nous sommes bien loin de notre but.

Keywords

32N1014xx
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 243 - 267
Copyright
Copyright © Canadian Mathematical Society 2007

References

Références

[A] Arthur, J., On some problems suggested by the trace formula. Dans: Lie Group Representations II, Lecture Notes in Math. 1041, Springer, Berlin, 1984, pp. 1–49.Google Scholar
[Br] Brieskorn, E., Sur les groupes de tresses. Séminaire Bourbaki 1971/72, No. 401.Google Scholar
[De] Deligne, P., Les immeubles des groupes de tresses généralisés. Invent. Math. 8(1972), 273–302.Google Scholar
[Ha] Harder, G., Eisensteinkohomologie und die Konstruktion gemischter Motive. Springer–Verlag, 1991.Google Scholar
[Hu] Hu, S.-T., Homotopy Theory. Academic Press, 1959.Google Scholar
[L1] Langlands, R. P., Problems in the theory of automorphic forms. In: Lectures in Modern Analysis and Applications, Lecture Notes in Math. 170, Springer–Verlag, 1970, 18–86.Google Scholar
[L2] Langlands, R. P., Where stands functoriality today? In: Representation Theory and Automorphic Forms, American Mathematical Society, Providence, RI, 1991, 457–471.Google Scholar
[L3] Langlands, R. P., Beyond endoscopy. In: Contributions to Automorphic Forms, Geometry and Number Theory, Johns Hopkins University Press, 2004, 611–698.Google Scholar
[N] Narkiewicz, W., The Development of Prime Number Theory. Springer–Verlag, 2000.Google Scholar