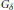Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tkachuk, Vladimir V.
2018.
Two point-picking games derived from a property of function spaces.
Quaestiones Mathematicae,
Vol. 41,
Issue. 6,
p.
729.
Aurichi, Leandro F.
and
Dias, Rodrigo R.
2019.
A minicourse on topological games.
Topology and its Applications,
Vol. 258,
Issue. ,
p.
305.
Clontz, Steven
and
Holshouser, Jared
2019.
Limited information strategies and discrete selectivity.
Topology and its Applications,
Vol. 265,
Issue. ,
p.
106815.
Jordan, Francis
2020.
On the instability of a topological game related to consonance.
Topology and its Applications,
Vol. 271,
Issue. ,
p.
106990.
Aurichi, Leandro F.
and
Duzi, Matheus
2021.
Topological games of bounded selections.
Topology and its Applications,
Vol. 291,
Issue. ,
p.
107449.
Osipov, Alexander V.
and
Özçağ, Selma
2021.
On the Alster, Menger and D-type covering properties.
Quaestiones Mathematicae,
Vol. 44,
Issue. 3,
p.
369.
Tkachuk, V. V.
2023.
Discrete and disjoint shrinking properties of locally convex spaces.
Acta Mathematica Hungarica,
Vol. 170,
Issue. 2,
p.
709.
Gruenhage, Gary
and
Tkachuk, Vladimir V.
2024.
Discrete selectivity, shrinking properties, and disjoint local
π
-bases
.
Quaestiones Mathematicae,
Vol. 47,
Issue. 5,
p.
1079.
Camasca Fernández, Juan F.
2025.
Equivalences in selective topological games on the class of dense subsets in the space of continuous functions C(X).
Topology and its Applications,
Vol. 370,
Issue. ,
p.
109435.
Hernández-Gutiérrez, Rodrigo
and
Spadaro, Santi
2025.
Comparing functional countability and exponential separability.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 119,
Issue. 1,
Lara, Dione
and
Mezabarba, Renan
2025.
Remarks on selective and game versions of special classes of points.
Filomat,
Vol. 39,
Issue. 12,
p.
4241.