Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
HILLMAN, Jonathan A.
2011.
Geometric decompositions of 4-dimensional orbifold bundles.
Journal of the Mathematical Society of Japan,
Vol. 63,
Issue. 3,

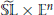 -Manifolds
-Manifolds