Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mortini, Raymond
and
Wick, Brett
2010.
Spectral characteristics and stable ranks for the Sarason algebra $H^\inf + C$.
Michigan Mathematical Journal,
Vol. 59,
Issue. 2,
Rupp, R.
and
Sasane, A.
2010.
On the stable rank and reducibility in algebras of real symmetric functions.
Mathematische Nachrichten,
Vol. 283,
Issue. 8,
p.
1194.
Mortini, Raymond
and
Rupp, Rudolf
2016.
Reducibility of invertible tuples to the principal component in commutative Banach algebras.
Arkiv för Matematik,
Vol. 54,
Issue. 2,
p.
499.

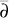 -Equation
-Equation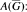 : Suppose that for
: Suppose that for 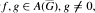 there exists δ > 0 such that
there exists δ > 0 such that 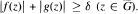 . Then there exist
. Then there exist 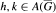 such that
such that