No CrossRef data available.
Article contents
Splitting Patterns and Trace Forms
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The splitting pattern of a quadratic form 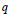 $q$ over a field
$q$ over a field 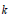 $k$ consists of all distinct Witt indices that occur for
$k$ consists of all distinct Witt indices that occur for 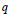 $q$ over extension fields of
$q$ over extension fields of 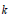 $k$ . In small dimensions, the complete list of splitting patterns of quadratic forms is known. We show that all splitting patterns of quadratic forms of dimension at most nine can be realized by trace forms.
$k$ . In small dimensions, the complete list of splitting patterns of quadratic forms is known. We show that all splitting patterns of quadratic forms of dimension at most nine can be realized by trace forms.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
1.
Bayer-Fluckiger, E., Galois Cohomology and the Trace Form. Jber. Dt. Math.-Verein. 96 (1994), 35–55.Google Scholar
2.
Conner, P. E. and Perlis, R., A Survey of Trace Forms of Algebraic Number Fields. World Scient. Publ. 2, Singapore, 1984.Google Scholar
3.
Delzant, A., Définition des Classes de Stiefel-Whitney d’un Module Quadratique sur un Corps Caractéristique Différente de 2. C. R. Acad. Sci. Paris 255 (1962), 1366–1368.Google Scholar
5.
Epkenhans, M. and Krüskemper, M., On Trace Forms of ´Etale Algebras and Field Extensions. Math. Z. 217 (1994), 421–433.Google Scholar
6.
Hoffmann, D. W., Isotropy of Quadratic Forms over the Function Field of a Quadric. Math. Z. 220 (1995), 461–466.Google Scholar
7.
Hoffmann, D. W., Splitting of Quadratic Forms, I: Forms of Small Dimension. preprint (1995).Google Scholar
8.
Hurrelbrink, J. and Rehmann, U., Splitting Patterns of Excellent Quadratic Forms. J. Reine Angew. Math. 444 (1993), 183–192.Google Scholar
9.
Hurrelbrink, J. and Rehmann, U., Splitting Patterns of Quadratic Forms. Math. Nachr. 176 (1995), 111–127.Google Scholar
11.
Izhboldin, O., On the Isotropy of Quadratic Forms over the Function Field of a Quadric. Algebra i Analiz (1) 10(1998), 21 pp.Google Scholar
12.
Knebusch, M., Generic Splitting of Quadratic Forms, I. Proc. London Math. Soc. 33 (1976), 65–93.Google Scholar
13.
Knebusch, M., Generic Splitting of Quadratic Forms, II. Proc. London Math. Soc. 34 (1977), 1–31.Google Scholar
14.
Mestre, J.-F., Extensions Régulières de Q(t) de Groupe de Galois An. J. Algebra 131 (1990), 483–495.Google Scholar
15.
Serre, J.-P., L’invariant de Witt de la Forme Tr(x2). Comment. Math. Helv. 59 (1984), 651–676.Google Scholar

