No CrossRef data available.
Article contents
The Spectrum and Isometric Embeddings of Surfaces of Revolution
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A sharp upper bound on the first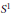 
${{S}^{1}}$ invariant eigenvalue of the Laplacian for 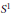${{S}^{1}}$ invariant metrics on 
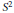${{S}^{2}}$ is used to find obstructions to the existence of 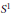${{S}^{1}}$ equivariant isometric embeddings of such metrics in ( 
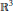${{\mathbb{R}}^{3}}$ , can). As a corollary we prove: If the first four distinct eigenvalues have even multiplicities then the metric cannot be equivariantly, isometrically embedded in ( 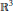${{\mathbb{R}}^{3}}$ , can). This leads to generalizations of some classical results in the theory of surfaces.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006
References
[1]
Abreu, M. and Freitas, P., On the invariant spectrum of S
1
-invariant metrics on S
2
.
Proc. London Math. Soc.
84(2002), 213–230.Google Scholar
[3]
Besse, A., Manifolds All of Whose Geodesics are Closed. Ergebnisse der Mathematik und ihrer Grenzgebiete 93, Springer-Verlag, Berlin, 1978.Google Scholar
[4]
Chen, B.-Y., A report on submanifolds of finite type.
Soochow J. Math.
22(1996), no. 2, 117–337.Google Scholar
[5]
Engman, M., New spectral characterization theorems for S
2
.
Pacific J. Math.
154(1992), no. 2, 215–229.Google Scholar
[6]
Engman, M., Trace formulae for S
1
invariant Green's operators on S
1
.
Manuscripta Math.
93(1997), no. 3, 357–368.Google Scholar
[7]
Engman, M., Sharp bounds for eigenvalues and multiplicities on surfaces of revolution.
Pacific J. Math.
186(1998), no. 1, 29–37.Google Scholar
[8]
Engman, M., A note on isometric embeddings of surfaces of revolution.
Amer.Math. Monthly
111(2004), no. 3, 251–255.Google Scholar
[9]
Greene, R., Metrics and isometric embeddings of the 2-sphere.
J. Differential Geometry
5(1971), 353–356.Google Scholar
[10]
Guan, P. and Li, Y. Y., The Weyl problem with nonnegative Gauss curvature.
J. Differential Geometry
39(1994), 331–342.Google Scholar
[12]
Hersch, M. J., Quatre propriétés isopérimétriques de membranes sphériques homogènes. C. R. Acad. Sci. Paris Sér. A-B 270(1970), A1645–A1648.Google Scholar
[13]
Hong, J. and Zuily, C., Isometric embedding of the 2-sphere with non negative curvature in ℝ3
.
Math. Z.
219(1995), no. 3, 323–334.Google Scholar
[14]
Hwang, A. D., A Symplectic Look at Surfaces of Revolution.
Enseign. Math. (2)
49(2003), no. 1-2, 157–172.Google Scholar
[15]
Hwang, A. and Singer, M., A momentum construction for circle-invariant Kähler metrics.
Trans. Amer.Math. Soc.
354(2002), 2285–2325.Google Scholar
[16]
Kobayashi, S., Transformation Groups in Differential Geometry. Reprint of the 1972 edition. Classics in Mathematics. Springer-Verlag, Heidelberg, 1995.Google Scholar
[17]
Lewy, H., A priori limitations for solutions of Monge–Ampère equations.
Trans. Amer. Math. Soc. (3)
37(1935), no. 3, 417–434.Google Scholar
[18]
Li, P. and Yau, S. T., A new conformal invariant and its applications to theWillmore Conjecture and the first eigenvalue of compact surfaces.
Invent. Math.
69(1982), no. 2, 269–291.Google Scholar
[19]
Nirenberg, L., The Weyl and Minkowski problems in differential geometry in the large.
Comm. Pure Appl. Math
6(1953), 337–394.Google Scholar
[20]
Pogorelov, A. V., Deformation of convex surfaces. Gosudarstv. Izdat. Tehn.-Teor. Lit., Moscow, 1951.Google Scholar
[21]
Pogorelov, A. V., Extrinsic geometry of convex surfaces. Translations of Mathematical Monographs 35, American Mathematical Society, Providence, RI, 1973.Google Scholar
[22]
Weyl, H., Über die Bestimmung einer geschlossen konvexen Fläche durch ihr Linienelement.
Vierteljahrschrift Naturforsch. Gesell, Zürich, 61(1916), 40–72.Google Scholar
[23]
Yau, S. T., Survey on partial differential equations in differential geometry. In: Seminar on Differential Geometry, Ann. of Math. Stud. 102, Princeton University Press, Princeton, NJ, 1982, pp. 3–71..Google Scholar
You have
Access