Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-27T14:49:40.801Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Spaces are not the Domain of a Closed Linear Operator in a Banach Space

Published online by Cambridge University Press:  20 November 2018

Peter Dierolf  and
Susanne Dierolf
Peter Dierolf
Affiliation:
Mathematisches Institut der Universität München Theresienstr. 39, D-800 München 2West Germany
Susanne Dierolf
Affiliation:
Mathematisches Institut der Universität München Theresienstr. 39, D-800 München 2West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 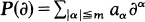be a linear partial differential operator with C∞- coefficients. The study of P(∂) as an operator in L2(ℝn) usually starts with the investigation of the minimal operator P0 which is the closure of P(∂) acting on . In the case of constant coefficients it is known that the domain D(P0) of P0 at least contains the space 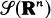(cf. Schechter [4, p. 58, Lemma 1.2]).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 501 - 503
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Diestel, J. and Uhl, J. J. Jr, Vector measures, American Mathematical Society, Providence, Rhode Island 1977.Google Scholar
2. Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Memoirs of the AMS, No. 16, American Mathematical Society, Providence, Rhode Island 1966.Google Scholar
3. Horvâth, J., Topological vector spaces and distributions, vol. I, Addison-Wesley Publishing Comp., Reading, Massachusetts 1966.Google Scholar
4. Schechter, M., Spectra of partial differential operators, North-Holland Publishing Comp., Amsterdam 1971.Google Scholar
5. Schwartz, L., Théorie des distributions, Hermann, Paris 1966.Google Scholar
6. Treves, F., Linear partial differential equations with constant coefficients, Gordon and Breach, New York 1966.Google Scholar
7. Valdivia, M., Absolutely convex sets in barrelled spaces, Ann. Inst. Fourier Grenoble 21, 1971, pp. 3-13.Google Scholar