Article contents
Some Results on Annihilating-ideal Graphs
Published online by Cambridge University Press: 20 November 2018
Abstract
The annihilating-ideal graph of a commutative ring 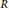 $R$ , denoted by
$R$ , denoted by 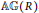 $\mathbb{A}\mathbb{G}\left( R \right)$ , is a graph whose vertex set consists of all non-zero annihilating ideals and two distinct vertices
$\mathbb{A}\mathbb{G}\left( R \right)$ , is a graph whose vertex set consists of all non-zero annihilating ideals and two distinct vertices  $I$ and
$I$ and 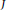 $J$ are adjacent if and only if
$J$ are adjacent if and only if 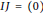 $IJ\,=\,\left( 0 \right)$ . Here we show that if
$IJ\,=\,\left( 0 \right)$ . Here we show that if 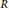 $R$ is a reduced ring and the independence number of
$R$ is a reduced ring and the independence number of 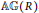 $\mathbb{A}\mathbb{G}\left( R \right)$ is finite, then the edge chromatic number of
$\mathbb{A}\mathbb{G}\left( R \right)$ is finite, then the edge chromatic number of 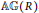 $\mathbb{A}\mathbb{G}\left( R \right)$ equals its maximum degree and this number equals
$\mathbb{A}\mathbb{G}\left( R \right)$ equals its maximum degree and this number equals 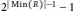 ${{2}^{\left| \min \left( R \right) \right|-1}}-\,1$ ; also, it is proved that the independence number of
${{2}^{\left| \min \left( R \right) \right|-1}}-\,1$ ; also, it is proved that the independence number of 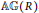 $\mathbb{A}\mathbb{G}\left( R \right)$ equals
$\mathbb{A}\mathbb{G}\left( R \right)$ equals 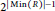 ${{2}^{\left| \min \left( R \right) \right|-1}}$ , where
${{2}^{\left| \min \left( R \right) \right|-1}}$ , where 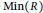 $\min \left( R \right)$ denotes the set of minimal prime ideals of
$\min \left( R \right)$ denotes the set of minimal prime ideals of 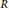 $R$ . Then we give some criteria for a graph to be isomorphic with an annihilating-ideal graph of a ring. For example, it is shown that every bipartite annihilating-ideal graph is a complete bipartite graph with at most two horns. Among other results, it is shown that a finite graph
$R$ . Then we give some criteria for a graph to be isomorphic with an annihilating-ideal graph of a ring. For example, it is shown that every bipartite annihilating-ideal graph is a complete bipartite graph with at most two horns. Among other results, it is shown that a finite graph 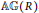 $\mathbb{A}\mathbb{G}\left( R \right)$ is not Eulerian, and that it is Hamiltonian if and only if
$\mathbb{A}\mathbb{G}\left( R \right)$ is not Eulerian, and that it is Hamiltonian if and only if 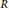 $R$ contains no Gorenstain ring as its direct summand.
$R$ contains no Gorenstain ring as its direct summand.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 4
- Cited by

