Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Betancor, J.J.
and
Marrero, I.
1995.
Algebraic Characterization of Convolution and Multiplication Operators on Hankel-Transformable Function and Distribution Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 4,
Betancor, J. J.
and
Marrero, I.
1997.
Convolution operators on Kucera-type spaces for the Hankel transformation.
Czechoslovak Mathematical Journal,
Vol. 47,
Issue. 1,
p.
47.
Betancor, Jorge J.
and
Rodíguez-Mesa, Lourdes
1997.
On Hankel convolutors on certain Hankel transformable function spaces.
Glasgow Mathematical Journal,
Vol. 39,
Issue. 3,
p.
351.
Betancor, Jorge J
and
Rodrı́guez-Mesa, Lourdes
1998.
Hankel Transformation of Colombeau Type Tempered Generalized Functions.
Journal of Mathematical Analysis and Applications,
Vol. 217,
Issue. 1,
p.
293.
Betancor, Jorge J.
and
Rodríguez-Mesa, Lourdes
1999.
On Hankel Convolution Equations in Distribution Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 29,
Issue. 1,
Betancor, J.J
and
Rodrı́guez-Mesa, L
1999.
A Paley–Wiener Theorem for the Hankel Transform of Colombeau Type Generalized Functions.
Journal of Mathematical Analysis and Applications,
Vol. 230,
Issue. 1,
p.
11.
Belhadj, M.
and
Betancor, J.J.
2002.
Hankel convolution operators on entire functions and distributions.
Journal of Mathematical Analysis and Applications,
Vol. 276,
Issue. 1,
p.
40.
Betancour, J.D.
Betancour, J.J.
and
Méndez, J.M.R.
2007.
Convolution Operators on Schwartz Spaces for Chébli-Trimèche Hypergroups.
Rocky Mountain Journal of Mathematics,
Vol. 37,
Issue. 3,
Pathak, R.S.
Prasad, Akhilesh
and
Kumar, Manish
2011.
n-Dimensional Sobolev type spaces involving Hankel transformation.
Applied Mathematics and Computation,
Vol. 218,
Issue. 3,
p.
899.
Upadhyay, Santosh Kumar
and
Maurya, Jay Singh
2021.
Continuous Bessel wavelet transform of distributions.
Rocky Mountain Journal of Mathematics,
Vol. 51,
Issue. 4,
Maurya, Jay Singh
and
Upadhyay, Santosh Kumar
2022.
The Bessel wavelet transform of distributions in βμ′-space.
International Journal of Wavelets, Multiresolution and Information Processing,
Vol. 20,
Issue. 04,
MAURYA, JAY SINGH
and
UPADHYAY, SANTOSH KUMAR
2023.
CHARACTERIZATIONS OF THE INVERSION FORMULA OF THE CONTINUOUS BESSEL WAVELET TRANSFORM OF DISTRIBUTIONS IN Hμ′(ℝ+).
Fractals,
Vol. 31,
Issue. 02,
Singh, Abhishek
and
Raghuthaman, Nikhila
2024.
Wavelet convolutors on the space of distributions.
Integral Transforms and Special Functions,
Vol. 35,
Issue. 11,
p.
626.

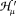 be the Zemanian space of Hankel transformable generalized functions and let
be the Zemanian space of Hankel transformable generalized functions and let 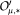 be the space of Hankel convolution operators for
be the space of Hankel convolution operators for 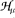 of
of 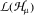 and in
and in 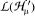 that commute with Hankel translations. Moreover, necessary and sufficient conditions on the generalized Hankel transform
that commute with Hankel translations. Moreover, necessary and sufficient conditions on the generalized Hankel transform 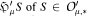 are established in order that every
are established in order that every 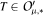 such that
such that 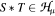 in
in 