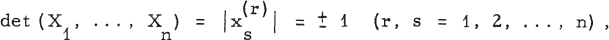Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1969.
Geometry of Numbers.
p.
471.
Malyshev, A. V.
and
Podsypanin, E. V.
1976.
Analytic methods in the theory of systems of diophantine equations and inequalities with a large number of unknowns.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 6,
p.
753.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.

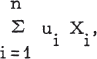 where u
where u