Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bešlagić, Amer
and
Rudin, Mary Ellen
1985.
Set-theoretic constructions of nonshrinking open covers.
Topology and its Applications,
Vol. 20,
Issue. 2,
p.
167.
Le Donne, Attilio
1985.
Shrinking property in Σ-products of paracompact p-spaces.
Topology and its Applications,
Vol. 19,
Issue. 2,
p.
95.
Bešlagić, Amer
1986.
Normality in products.
Topology and its Applications,
Vol. 22,
Issue. 1,
p.
71.
Yasui, Yoshikazu
1989.
Topics in General Topology.
Vol. 41,
Issue. ,
p.
161.
BESLAGIC, AMER
1993.
Normality in Products.
Annals of the New York Academy of Sciences,
Vol. 705,
Issue. 1,
p.
17.
Yajima, Yukinobu
1993.
Subnormality of X × κ and Σ-products.
Topology and its Applications,
Vol. 54,
Issue. 1-3,
p.
111.
Yang, Le Cheng
1994.
Countable paracompactness of Σ-products.
Proceedings of the American Mathematical Society,
Vol. 122,
Issue. 3,
p.
949.
Tanaka, Hidenori
and
Yajima, Yukinobu
2002.
Σ-products of paracompact C-scattered spaces.
Topology and its Applications,
Vol. 124,
Issue. 1,
p.
39.
Chiba, Keiko
2003.
Encyclopedia of General Topology.
p.
37.
Gao, Y. -Z.
Qu, H. -Z.
and
Wang, S. -T.
2007.
A note on monotonically normal spaces.
Acta Mathematica Hungarica,
Vol. 117,
Issue. 1-2,
p.
175.
Clontz, Steven
and
Gruenhage, Gary
2014.
Proximal compact spaces are Corson compact.
Topology and its Applications,
Vol. 173,
Issue. ,
p.
1.
Bell, Jocelyn R.
2014.
An infinite game with topological consequences.
Topology and its Applications,
Vol. 175,
Issue. ,
p.
1.
Morgan, Charles J.G.
Rangel, Dimi R.
and
da Silva, Samuel G.
2017.
Almost disjoint families and relative versions of covering properties of κ-paracompactness type.
Topology and its Applications,
Vol. 221,
Issue. ,
p.
476.
Bell, Jocelyn R.
2018.
A variation of the proximal infinite game.
Topology and its Applications,
Vol. 242,
Issue. ,
p.
43.

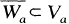 for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.
for each a ∈ A.lt is strangely difficult to find an example of a normal space without the shrinking property. It is proved here that any ∑-product of metric spaces has the shrinking property.