Article contents
Sharp Inequalities for Differentially Subordinate Harmonic Functions and Martingales
Published online by Cambridge University Press: 20 November 2018
Abstract
We determine the best constants 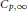 ${{C}_{p,\infty }}$ and
${{C}_{p,\infty }}$ and 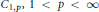 ${{C}_{1,p}},\,1\,<\,p\,<\,\infty $ , for which the following holds. If
${{C}_{1,p}},\,1\,<\,p\,<\,\infty $ , for which the following holds. If 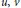 $u,v$ are orthogonal harmonic functions on a Euclidean domain such that
$u,v$ are orthogonal harmonic functions on a Euclidean domain such that  $v$ is differentially subordinate to
$v$ is differentially subordinate to  $u$ , then
$u$ , then
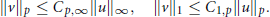 $${{\left\| v \right\|}_{p}}\le {{C}_{p}}{{,}_{\infty }}{{\left\| u \right\|}_{\infty }},\,\,\,\,\,\,\,\,\,\,\,{{\left\| v \right\|}_{1}}\le {{C}_{1,p}}{{\left\| u \right\|}_{p}}.$$
$${{\left\| v \right\|}_{p}}\le {{C}_{p}}{{,}_{\infty }}{{\left\| u \right\|}_{\infty }},\,\,\,\,\,\,\,\,\,\,\,{{\left\| v \right\|}_{1}}\le {{C}_{1,p}}{{\left\| u \right\|}_{p}}.$$
In particular, the inequalities are still sharp for the conjugate harmonic functions on the unit disc of 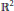 ${{\mathbb{R}}^{2}}$ . Sharp probabilistic versions of these estimates are also studied. As an application, we establish a sharp version of the classical logarithmic inequality of Zygmund.
${{\mathbb{R}}^{2}}$ . Sharp probabilistic versions of these estimates are also studied. As an application, we establish a sharp version of the classical logarithmic inequality of Zygmund.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 1
- Cited by

