No CrossRef data available.
Article contents
Sets of Uniqueness for Univalent Functions
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We observe that any set of uniqueness for the Dirichlet space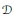 
$\mathcal{D}$ is a set of uniqueness for the class 
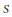$S$ of normalized univalent holomorphic functions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
[1]
Bogdan, K., On the zeros of functions with finite Dirichlet integral. Kodai Math. J. 19 (1996), 7–16.Google Scholar
[2]
Caughran, J. G., Two results concerning the zeros of functions with finite Dirichlet integral. Canad. J. Math. 21 (1969), 312–316.Google Scholar
[4]
Duren, P. L., Problem 6.83. In: Research Problems in Complex Analysis (Eds. K. F. Barth, D. A. Brannan and W. K. Hayman), Bull. Lond.Math. Soc. 16 (1984), 490–517.Google Scholar
[5]
Lappan, P., Points Where Univalent Functions May Coincide. Complex Variables 5 (1985), 17–20.Google Scholar
[6]
Nagel, A., Rudin, W. and Shapiro, J. H., Tangential boundary behavior of functions in Dirichlet-type spaces. Ann. of Math. 116 (1982), 331–360.Google Scholar
[7]
Obrock, A., Problem 2.2. In: Problems in Complex Function Theory (Ed. Ch. Pommerenke), Bull. Lond. Math. Soc. 4 (1972), 354–366.Google Scholar
[8]
Shapiro, H. S. and Shields, A. L., On the zeros of functions with finite Dirichlet integral and some related function spaces. Math. Z. 80 (1962), 217–229.Google Scholar
[9]
Stegbuchner, H., Carleson sets and fixed-points of schlicht functions. Romanian-Finnish Seminar in Complex Analysis (Proc., Bucharest, 1976), 373–388, Lecture Notes in Math. 743, Springer-Verlag, Berlin, 1979.Google Scholar
You have
Access