Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lledó, Fernando
and
Yakubovich, Dmitry V.
2013.
Følner sequences and finite operators.
Journal of Mathematical Analysis and Applications,
Vol. 403,
Issue. 2,
p.
464.
Ara, Pere
Lledó, Fernando
and
Yakubovich, Dmitry V.
2014.
Operator Theory, Operator Algebras and Applications.
Vol. 242,
Issue. ,
p.
1.

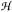 is called finite if
is called finite if 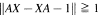 for each
for each 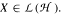 . It is shown that the class of all finite operators is a closed nowhere dense subset of
. It is shown that the class of all finite operators is a closed nowhere dense subset of