Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Assem, Ibrahim
and
Skowroński, Andrzej
1988.
Algebras with cycle-finite derived categories.
Mathematische Annalen,
Vol. 280,
Issue. 3,
p.
441.
Assem, Ibrahim
and
Skowronski, Andrzej
1989.
Séminaire d’Algèbre Paul Dubreil et Marie-Paul Malliavin.
Vol. 1404,
Issue. ,
p.
1.
Zhang, Chao
and
Han, Yang
2016.
Brauer-Thrall Type Theorems for Derived Module Categories.
Algebras and Representation Theory,
Vol. 19,
Issue. 6,
p.
1369.
Chaio, Claudia
and
Guazzelli, Victoria
2020.
On the Radical of the Module Category of an Endomorphism Algebra.
Algebras and Representation Theory,
Vol. 23,
Issue. 3,
p.
1159.

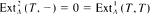 and there exists an exact sequence 0 → A
and there exists an exact sequence 0 → A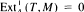 (respectively,
(respectively, 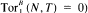 . We prove that
. We prove that 