No CrossRef data available.
Article contents
A Second Note on Ingham's Summation Method
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A series ∑ an is said to be summable (I) to the limit A if
(*)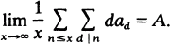
Clearly the limit is the same whether x→∞ through all real values or only positive integer values, and the expression whose limit is being taken can also be expressed in the two equivalent forms
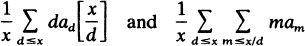
where [x] is the greatest integer ≤x.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979
References
1. Erdös, P. and Segal, S. L., A note on Ingham's Summation Method, Jour. Number Theory, 10, (1978), 95-98.Google Scholar
3.
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Oxford (4th edition, 1965).Google Scholar
4.
Ingham, A. E., Some Tauberian Theorems connected with the Prime Number Theorem, J. London Math. Soc.
20, (1945), 171-180.Google Scholar
5.
Rubel, L. A., An Abelian Theorem for Number-Theoretic Sums, Acta Arithmetica
6, (1960), 175-177, Correction Acta Arithmetica 6, (1961), 523.Google Scholar
6.
Segal, S. L., Ingham's Summation Method and the Riemann Hypothesis, Proc. Lond. Math. Soc. (3) 30, (1975), 129-142, Carrijendum 34 (1977), 438.Google Scholar
7.
Segal, S. L., On Ingham's Summation Method, Canadian Journal Math., 18, (1966), 97-105.Google Scholar

