Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T09:58:14.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Sampling and interpolation for the discrete Hilbert and Kak–Hilbert transforms

Part of: Groups and semigroups of linear operators, their generalizations and applications Integral transforms, operational calculus

Published online by Cambridge University Press:  07 March 2022

Isaac Z. Pesenson Open the ORCID record for Isaac Z. Pesenson [Opens in a new window]
Isaac Z. Pesenson*
Affiliation:
Department of Mathematics, Temple University, Philadelphia, PA, 19122 USA
*
e-mail: pesenson@temple.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of the paper is to obtain analogs of the sampling theorems and of the Riesz–Boas interpolation formulas which are relevant to the discrete Hilbert and Kak–Hilbert transforms in 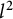$l^{2}$ .

Keywords

Discrete Hilbert transformKak–Hilbert transformone-parameter groups of operatorssamplingRiesz–Boas interpolation

MSC classification

Primary: 47D03: Groups and semigroups of linear operators
Secondary: 44A15: Special transforms (Legendre, Hilbert, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 395 - 410
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhiezer, J., Theory of approximation, Ungar, New York, 1956.Google Scholar
Boas, R., The derivative of a trigonometric integral . J. Lond. Math. Soc. 164(1937), 1–12.Google Scholar
Boas, R., Entire functions, Academic Press, New York, 1954.Google Scholar
Butzer, P. and Berens, H., Semi-groups of operators and approximation, Springer, Berlin, 1967.10.1007/978-3-642-46066-1CrossRefGoogle Scholar
Butzer, P. L., Ferreira, P. J. S. G., Higgins, J. R., Schmeisser, G., and Stens, R. L., The sampling theorem, Poisson summation formula, general Parseval formula, reproducing kernel formula and the Paley–Wiener theorem for bandlimited signals—their interconnections . Appl. Anal. 90(2011), nos. 3–4, 431–461.10.1080/00036811003627567CrossRefGoogle Scholar
Butzer, P. L., Schmeisser, G., and Stens, R. L., Shannon sampling theorem for bandlimited signals and their Hilbert transform, Boas-type formulae for higher order derivatives. The aliasing error involved by their extensions from bandlimited to non-bandlimited signals . Entropy 14(2012), 2192–2226. https://doi.org/10.3390/e14112192 CrossRefGoogle Scholar
De Carli, L. and Samad, S., One-parameter groups and discrete Hilbert transform . Can. Math. Bull. 59(2016), 497–507.10.4153/CMB-2016-028-7CrossRefGoogle Scholar
Grafakos, L., An elementary proof of the square summability of the discrete Hilbert transform . Amer. Math. Monthly 101(1994), 456–458.10.1080/00029890.1994.11996974CrossRefGoogle Scholar
Higgins, J. R., A sampling theorem for irregular sample points . IEEE Trans. Inform. Theory 22(1976), 621–622.10.1109/TIT.1976.1055596CrossRefGoogle Scholar
Kak, S., The discrete Hilbert transform . Proc. IEEE 58(1970), 585–586.CrossRefGoogle Scholar
Krein, S. G., Linear differential equations in Banach space, Translations of Mathematical Monographs, 29, American Mathematical Society, Providence, RI, 1971, v+390 pp.Google Scholar
Nikol’skii, S., Approximation of functions of several variables and imbedding theorems, Springer, Berlin, 1975.10.1007/978-3-642-65711-5CrossRefGoogle Scholar
Pesenson, I. Z., Boas-type formulas and sampling in Banach spaces with applications to analysis on manifolds . In: New perspectives on approximation and sampling theory, Springer International Publishing, Cham, 2014, pp. 39–61.10.1007/978-3-319-08801-3_3CrossRefGoogle Scholar
Pesenson, I. Z., Sampling formulas for groups of operators in Banach spaces . Sampl. Theory Signal Image Process. 14(2015), no. 1, 1–16.CrossRefGoogle Scholar
Riesz, M., Eine trigonometrische Interpolationsformel und einige Ungleichungen für Polynome . Jahresber. Deutsch. Math.-Verein. 23(1914), 354–368.Google Scholar
Riesz, M., Les fonctions conjuguees et les series de Fourier. C. R. Acad. Sci. 178(1924), 1464–1467.Google Scholar
Schmeisser, G., Numerical differentiation inspired by a formula of R. P. Boas . J. Approx. Theory 160(2009), 202–222.10.1016/j.jat.2008.04.005CrossRefGoogle Scholar
Schur, I., Bemerkungen zur Theorie der beschran̈kten Bilinearformen mit unendlich vielen Veran̈derlichen . J. Reine Angew. Math. 140(1911), 1–28.10.1515/crll.1911.140.1CrossRefGoogle Scholar