Article contents
Rigidity of Hamiltonian Actions
Published online by Cambridge University Press: 20 November 2018
Abstract
This paper studies the following question: Given an 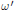 ${\omega }'$ -symplectic action of a Lie group on a manifold
${\omega }'$ -symplectic action of a Lie group on a manifold 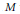 $M$ which coincides, as a smooth action, with a Hamiltonian
$M$ which coincides, as a smooth action, with a Hamiltonian 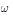 $\omega$ -action, when is this action a Hamiltonian
$\omega$ -action, when is this action a Hamiltonian 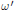 ${\omega }'$ -action? Using a result of Morse-Bott theory presented in Section 2, we show in Section 3 of this paper that such an action is in fact a Hamiltonian
${\omega }'$ -action? Using a result of Morse-Bott theory presented in Section 2, we show in Section 3 of this paper that such an action is in fact a Hamiltonian 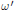 ${\omega }'$ -action, provided that
${\omega }'$ -action, provided that 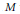 $M$ is compact and that the Lie group is compact and connected. This result was first proved by Lalonde-McDuff-Polterovich in 1999 as a consequence of a more general theory that made use of hard geometric analysis. In this paper, we prove it using classical methods only.
$M$ is compact and that the Lie group is compact and connected. This result was first proved by Lalonde-McDuff-Polterovich in 1999 as a consequence of a more general theory that made use of hard geometric analysis. In this paper, we prove it using classical methods only.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 2
- Cited by

