No CrossRef data available.
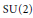 $\text{SU(2)}$-Valued Moment Maps
$\text{SU(2)}$-Valued Moment MapsPublished online by Cambridge University Press: 20 November 2018
Jeffrey and Kirwan gave expressions for intersection pairings on the reduced space 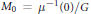 ${{M}_{0\,}}=\,{{\mu }^{-1}}(0)/G$ of a Hamiltonian
${{M}_{0\,}}=\,{{\mu }^{-1}}(0)/G$ of a Hamiltonian  $G$-space
$G$-space 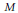 $M$ in terms of multiple residues. In this paper we prove a residue formula for symplectic volumes of reduced spaces of a quasi-Hamiltonian
$M$ in terms of multiple residues. In this paper we prove a residue formula for symplectic volumes of reduced spaces of a quasi-Hamiltonian 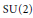 $\text{SU(2)}$-space. The definition of quasi-Hamiltonian
$\text{SU(2)}$-space. The definition of quasi-Hamiltonian  $G$-spaces was introduced by Alekseev, Malkin and Meinrenken.
$G$-spaces was introduced by Alekseev, Malkin and Meinrenken.