Article contents
Remarks on Certain Metaplectic Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
We study metaplectic coverings of the adelized group of a split connected reductive group 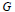 $G$ over a number field
$G$ over a number field 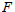 $F$ . Assume its derived group
$F$ . Assume its derived group 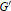 ${G}'$ is a simply connected simple Chevalley group. The purpose is to provide some naturally defined sections for the coverings with good properties which might be helpful when we carry some explicit calculations in the theory of automorphic forms on metaplectic groups. Specifically, we
${G}'$ is a simply connected simple Chevalley group. The purpose is to provide some naturally defined sections for the coverings with good properties which might be helpful when we carry some explicit calculations in the theory of automorphic forms on metaplectic groups. Specifically, we
-
1. construct metaplectic coverings of
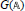 $G(\mathbb{A})$ from those of
$G(\mathbb{A})$ from those of 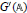 ${G}'\,(\mathbb{A})$ ;
${G}'\,(\mathbb{A})$ ; -
2. for any non-archimedean place
 $v$ , show the section for a covering of
$v$ , show the section for a covering of 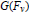 $G\,({{F}_{v}})$ constructed from a Steinberg section is an isomorphism, both algebraically and topologically in an open subgroup of
$G\,({{F}_{v}})$ constructed from a Steinberg section is an isomorphism, both algebraically and topologically in an open subgroup of 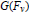 $G\,({{F}_{v}})$ ;
$G\,({{F}_{v}})$ ; -
3. define a global section which is a product of local sections on a maximal torus, a unipotent subgroup and a set of representatives for the Weyl group.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 1
- Cited by

