No CrossRef data available.
Article contents
Probabilistic Proofs of the Little Riesz Theorem
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The following theorem is a widely used corollary of the Thorn-Riesz convexity theorem ([1], pp. 526).
Theorem. Let (Ω, a, μ) be a positive measure space, and let
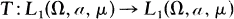
be a linear operator with ‖T‖1≤1, ‖T‖∞≤1. Then ‖T‖p≤1, 1≤p≤∞
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1977
References
2.
Hardy, G.H., Littlewood, J.E., and Polya, G., Inequalities. Cambridge University Press, 1952.Google Scholar
3.
Lacey, H.E., The isometric theory of classical Banach spaces, Berlin, Springer-Verlag, 1974.Google Scholar
4.
Rosenblatt, M., Markov processes; structure and asymptotic behavior, Berlin, Springer-Verlag, 1971.Google Scholar

