No CrossRef data available.
Article contents
Prime and Primary Ideals in a Prüfer Order in a Simple Artinian Ring with Finite Dimension over its Center
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 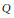 $Q$ be a simple Artinian ring with finite dimension over its center. An order
$Q$ be a simple Artinian ring with finite dimension over its center. An order 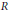 $R$ in
$R$ in 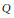 $Q$ is said to be Prüfer if any one-sided
$Q$ is said to be Prüfer if any one-sided 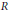 $R$ -ideal is a progenerator. We study prime and primary ideals of a Prüfer order under the condition that the center is Prüfer. Also we characterize branched and unbranched prime ideals of a Prüfer order.
$R$ -ideal is a progenerator. We study prime and primary ideals of a Prüfer order under the condition that the center is Prüfer. Also we characterize branched and unbranched prime ideals of a Prüfer order.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
[AD]
Alajbegovi`c, J. H. and Dubrovin, N. I., Non-commutative Prüfer rings. J. Algebra 135 (1990), 165–176.Google Scholar
[D1]
Dubrovin, N. I., Noncommutative valuation rings. Trans. MoscowMath. Soc. 45 (1984), 273–287.Google Scholar
[D2]
Dubrovin, N. I., Noncommutative valuation ring in simple finite-dimensional algebras over a field.Math. USSRSb. (2) 51 (1985), 493–505.Google Scholar
[G1]
Gräter, J., The defectsatz for central simple algebras. Trans. Amer.Math. Soc. (2) 330 (1992), 823–843.Google Scholar
[G2]
Gräter, J., Prime PI rings in which finitely generated right ideals are principal. Math. Forum 4 (1992), 447–463.Google Scholar
[L]
Lambek, J., Lectures on rings and modules. Chelsea Publishing Company, New York, 1986.Google Scholar
[MMU]
Marubayashi, H., Miyamoto, H. and Ueda, A., Prime ideals in noncommutative valuation rings in finite dimensional central simple algebras. Proc. Japan Acad. Ser. A Math. Sci. (2) 69 (1993), 35–40.Google Scholar
[MM1]
Marubayashi, H., Miyamoto, H., Ueda, A. and Zhao, Y., Semi-hereditary orders in a simple Artinian ring. Comm. Algebra (13) 22 (1994), 5209–5230.Google Scholar
[MM2]
Marubayashi, H., Miyamoto, H., Ueda, A. and Zhao, Y., On semi-local Bezout orders and strongly Prüfer orders in a central simple algebra. Math. Japon. (2) 43 (1996), 377–382.Google Scholar
[MY]
Marubayashi, H. and Yi, Z., Dubrovin valuation properties of skew group rings and crossed products. Comm. Algebra, to appear.Google Scholar
[M1]
Morandi, P. J., Maximal orders over valuation ring. J. Algebra 152 (1992), 313–341.Google Scholar
[M2]
Morandi, P. J., Noncommutative Prüfer rings satisfying a polynomial identity. J. Algebra 161 (1993), 324–341.Google Scholar

