Article contents
Positive Definiteness on Products of Compact Two-point Homogeneous Spaces and Locally Compact Abelian Groups
Published online by Cambridge University Press: 29 October 2019
Abstract
In this paper, we consider the problem of characterizing positive definite functions on compact two-point homogeneous spaces cross locally compact abelian groups. For a locally compact abelian group 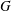 $G$ with dual group
$G$ with dual group 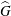 $\widehat{G}$, a compact two-point homogeneous space
$\widehat{G}$, a compact two-point homogeneous space  $\mathbb{H}$ with normalized geodesic distance
$\mathbb{H}$ with normalized geodesic distance 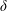 $\unicode[STIX]{x1D6FF}$ and a profile function
$\unicode[STIX]{x1D6FF}$ and a profile function 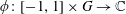 $\unicode[STIX]{x1D719}:[-1,1]\times G\rightarrow \mathbb{C}$satisfying certain continuity and integrability assumptions, we show that the positive definiteness of the kernel
$\unicode[STIX]{x1D719}:[-1,1]\times G\rightarrow \mathbb{C}$satisfying certain continuity and integrability assumptions, we show that the positive definiteness of the kernel 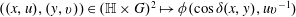 $((x,u),(y,v))\in (\mathbb{H}\times G)^{2}\mapsto \unicode[STIX]{x1D719}(\cos \unicode[STIX]{x1D6FF}(x,y),uv^{-1})$ is equivalent to the positive definiteness of the Fourier transformed kernels
$((x,u),(y,v))\in (\mathbb{H}\times G)^{2}\mapsto \unicode[STIX]{x1D719}(\cos \unicode[STIX]{x1D6FF}(x,y),uv^{-1})$ is equivalent to the positive definiteness of the Fourier transformed kernels 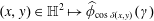 $(x,y)\in \mathbb{H}^{2}\mapsto \widehat{\unicode[STIX]{x1D719}}_{\cos \unicode[STIX]{x1D6FF}(x,y)}(\unicode[STIX]{x1D6FE})$,
$(x,y)\in \mathbb{H}^{2}\mapsto \widehat{\unicode[STIX]{x1D719}}_{\cos \unicode[STIX]{x1D6FF}(x,y)}(\unicode[STIX]{x1D6FE})$, 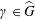 $\unicode[STIX]{x1D6FE}\in \widehat{G}$, where
$\unicode[STIX]{x1D6FE}\in \widehat{G}$, where 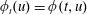 $\unicode[STIX]{x1D719}_{t}(u)=\unicode[STIX]{x1D719}(t,u)$,
$\unicode[STIX]{x1D719}_{t}(u)=\unicode[STIX]{x1D719}(t,u)$, 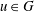 $u\in G$. We also provide some results on the strict positive definiteness of the kernel.
$u\in G$. We also provide some results on the strict positive definiteness of the kernel.
Keywords
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
Partially supported by FAPESP, grant 2016/09906-0.
References
- 3
- Cited by


