Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T17:49:15.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic Solutions of Second Order Degenerate Differential Equations with Delay in Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Shangquan Bu  and
Gang Cai
Shangquan Bu
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, China, e-mail : sbu@math.tsinghua.edu.cn
Gang Cai
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing, 401331, China, e-mail : caigang-aaaa@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give necessary and sufficient conditions of the 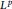${{L}^{p}}$ -well-posedness (resp. 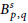$B_{p,\,q}^{s}$ -wellposedness) for the second order degenerate differential equation with finite delays

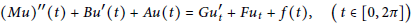$${{\left( Mu \right)}^{\prime \prime }}\left( t \right)+B{u}'\left( t \right)+Au\left( t \right)=G{{{u}'}_{t}}+F{{u}_{t}}+f\left( t \right),\left( t\in \left[ 0,2\pi\right] \right)$$

with periodic boundary conditions 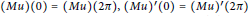$\left( Mu \right)\,\left( 0 \right)\,=\,\left( Mu \right)\,\left( 2\pi\right),\,{{\left( Mu \right)}^{\prime }}\left( 0 \right)\,=\,{{\left( Mu \right)}^{\prime }}\left( 2\pi\right)$ , where 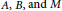$A,\,B,\,\text{and}\,M$ are closed linear operators on a complex Banach space 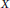$X$ satisfying 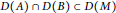$D\left( A \right)\,\cap \,D\left( B \right)\,\subset \,D\left( M \right)$ , 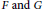$F\,\text{and}\,G$ are bounded linear operators from 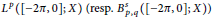${{L}^{p}}\left( \left[ -2\pi ,\,0 \right];\,X \right)\,\left( \text{resp}\text{.}\,\text{B}_{p,q}^{s}\left( \left[ -2\pi ,\,0 \right];\,X \right) \right)$ into 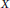$X$ .

Keywords

34G1034K3043A1547D06second order degenerate differential equationFourier multiplier theoremwellposednessLebesgue-Bochner spaceBesov space

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 717 - 737
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Arendt, W., Batty, C., Hieber, M., and Neubrander, E., Vector-valued Laplace transforms and Cauchy problems. Monographs in Mathematics, 96, Birkhâuser/Springer Basel AG, Basel, 2001. http://dx.doi.org/10.1007/978-3-0348-0087-7Google Scholar
[2] Arendt, W. and Bu, S., The operator-valued Marcinkiewicz multiplier theorem and maximal regularity. Math. Z. 240 (2002), 311–343. http://dx.doi.Org/10.1007/s002090100384Google Scholar
[3] Arendt, W. and Bu, S., Operator-valued Fourier multipliers on periodic Besov spaces and applications. Proc. Edinb. Math. Soc. 47 (2004), 15–33. http://dx.doi.org/10.1017/S0013091502000378Google Scholar
[4] Bu, S., Well-posedness of second order degenerate differential equations in vector-valued function spaces. Studia Math. 214 (2013), 1–16. http://dx.doi.org/10.4064/sm214-1-1Google Scholar
[5] Bu, S. and Cai, G., Well-posedness of second-order degenerate differential equations with finite delay. Proc. Edinb. Math. Soc. 60 (2017), 349–360. http://dx.doi.Org/10.1017/S0013091516000262Google Scholar
[6] Bu, S. and Fang, Y., Periodic solutions of delay equations in Besov spaces and Triebel-Lizorkin spaces. Taiwanese J. Math. 13 (2009), 1063–1076. http://dx.doi.Org/10.1165O/twjm/1500405460Google Scholar
[7] Bu, S. and Fang, Y., Maximal regularity of second order delay equations in Banach spaces. Sci China Math. 53 (2010), 51–62. http://dx.doi.Org/10.1007/s11425-009-0108-5Google Scholar
[8] Favini, A. and Yagi, A., Degenerate differential equations in Banach spaces. Monographs and Textbooks in Pure and Applied Mathematics, 215, Dekker, New York, 1999.Google Scholar
[9] Fu, X. and Li, M., Maximal regularity of second-order evolution equations with infinite delay in Banach spaces. Studia Math. 224 (2014), 199–219. http://dx.doi.Org/10.4064/sm224-3-2Google Scholar
[10] Keyantuo, V. and Lizama, C., Periodic solutions of second order differential equations in Banach spaces. Math. Z. 253 (2006), 489–514. http://dx.doi.Org/10.1007/s00209-005-0919-1Google Scholar
[11] Keyantuo, V. and Lizama, C., A characterization of periodic solutions for time fractional differential equations in UMD spaces and applications. Math. Nachr. 284 (2011), 494–506. http://dx.doi.org/10.1002/mana.200810158Google Scholar
[12] Lizama, C., Fourier multipliers and periodic solutions of delay equations in Banach spaces. J. Math. Anal. Appl. 324 (2006), 921–933. http://dx.doi.Org/10.1016/j.jmaa.2005.12.043Google Scholar
[13] Lizama, C. and Ponce, R., Periodic solutions of degenerate differential equations in vector-valued function spaces. Studia Math. 202 (2011), 49–63. http://dx.doi.Org/10.4064/sm202-1-3Google Scholar
[14] Lizama, C. and Ponce, R., Maximal regularity for degenerate differential equations with infinite delay in periodic vector-valued function spaces. Proc. Edinb. Math. Soc. 56 (2013), 853–871. http://dx.doi.Org/10.1017/S0013091513000606Google Scholar
[15] Poblete, V., Maximal regularity of second-order equations with delay. J. Differential Equations 246 (2009), 261–276. http://dx.doi.Org/10.1016/j.jde.2008.03.034Google Scholar
[16] V. Poblete and Pozo, J. C., Periodic solutions of an abstract third-order differential equations. Studia Math. 215 (2013), 195–219. http://dx.doi.org/10.4064/sm215-3-1Google Scholar
[17] Poblete, V. and Pozo, J. C., Periodic solutions of a fractional neutral equations with finite delay. J. Evol. Equ. 14 (2014), 417–444. http://dx.doi.Org/10.1007/S00028-014-0221-yGoogle Scholar
[18] Sviridyuk, G. and Fedorov, V., Linear type equations and degenerate semigroups of operators. Inverse and Ill-posed Problems Series, VSP, Utrecht, 2003. http://dx.doi.org/10.1515/9783110915501Google Scholar