Hostname: page-component-cb9f654ff-k7rjm Total loading time: 0 Render date: 2025-08-25T17:15:07.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal free export/import regions

Part of: Operations research and management science Manifolds

Published online by Cambridge University Press:  17 September 2020

Samer Dweik
Samer Dweik*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada
*
e-mail: dweik@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the problem of finding two free export/import sets 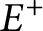$E^+$ and 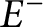$E^-$ that minimize the total cost of some export/import transportation problem (with export/import taxes 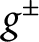$g^\pm $), between two densities 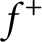$f^+$ and 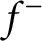$f^-$, plus penalization terms on 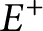$E^+$ and 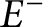$E^-$. First, we prove the existence of such optimal sets under some assumptions on 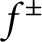$f^\pm $ and 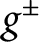$g^\pm $. Then we study some properties of these sets such as convexity and regularity. In particular, we show that the optimal free export (resp. import) region 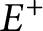$E^+$ (resp. 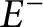$E^-$) has a boundary of class 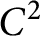$C^2$ as soon as 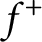$f^+$ (resp. 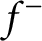$f^-$) is continuous and 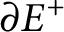$\partial E^+$ (resp. 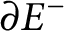$\partial E^-$) is 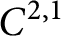$C^{2,1}$ provided that 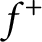$f^+$ (resp. 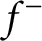$f^-$) is Lipschitz.

Keywords

Shape optimizationoptimal regionsimport/export transport problem

MSC classification

Primary: 49Q10: Optimization of shapes other than minimal surfaces
Secondary: 49Q20: Variational problems in a geometric measure-theoretic setting 90B20: Traffic problems

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 737 - 751
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Buttazzo, G., Carlier, G. and Guarino Lo Bianco, S., Optimal regions for congested transport . ESAIM Math. Model. Numer. Anal. 49(2015), 1607–1619. http://dx.doi.org/10.1051/m2an/2015022 CrossRefGoogle Scholar
Dweik, S., Optimal transportation with boundary costs and summability estimates on the transport density . J. Convex Anal. 25(2018), 135–160.Google Scholar
Dweik, S., Weighted Beckmann problem with boundary costs . Quart. Appl. Math. 76(2018), 601–609. http://dx.doi.org/10.1090/qam/1512 CrossRefGoogle Scholar
Dweik, S. and Santambrogio, F., Summability estimates on transport densities with Dirichlet regions on the boundary via symmetrization techniques . ESAIM Control Optim. Calc. Var. 24(2018), 1167–1180. http://dx.doi.org/10.1051/cocv/2017018 CrossRefGoogle Scholar
Dweik, S., Ghoussoub, N., and Palmer, A. Z., Optimal controlled transports with free end times subject to import/export tariffs . J. Dyn. Control Syst. 26(2020), 481–507. http://dx.doi.org/10.1007/s10883-019-09458-1 CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order . 2nd ed., Grundlehren der Mathematischen Wissenschaften, 224, Springer-Verlag, New York/Berlin, 1983. http://dx.doi.org/10.1007/978-3-642-61798-0 Google Scholar
Henrot, A. and Pierre, M., Variation et optimisation de formes. Une analyse géométrique . Mathématiques & Applications, 48, Springer-Verlag, Berlin, 2005. http://dx.doi.org/10.1007/3-540-37689-5 CrossRefGoogle Scholar
Mazon, J. M., Rossi, J., and Toledo, J., An optimal transportation problem with a cost given by the euclidean distance plus import/export taxes on the boundary . Rev. Mat. Iberoam. 30(2014), no. 1, 277–308. http://dx.doi.org/10.4171/RMI/778 CrossRefGoogle Scholar
Santambrogio, F., Optimal transport for applied mathematicians . In: Progress in nonlinear differential equations and their applications, 87, Birkhäuser Basel, 2015. http://dx.doi.org/10.1007/978-3-319-20828-2 Google Scholar