No CrossRef data available.
Article contents
On the Structure of the Schild Group in Relativity Theory
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Alfred Schild has established conditions that Lorentz transformationsmap world-vectors 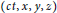 $(ct,x,y,z)$ with integer coordinates onto vectors of the same kind. These transformations are called integral Lorentz transformations.
$(ct,x,y,z)$ with integer coordinates onto vectors of the same kind. These transformations are called integral Lorentz transformations.
This paper contains supplements to our earlier work with a new focus on group theory. To relate the results to the familiar matrix group nomenclature, we associate Lorentz transformations with matrices in 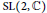 $\text{SL}(2,\mathbb{C})$ . We consider the lattice of subgroups of the group originated in Schild's paper and obtain generating sets for the full group and its subgroups.
$\text{SL}(2,\mathbb{C})$ . We consider the lattice of subgroups of the group originated in Schild's paper and obtain generating sets for the full group and its subgroups.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
[1]
Baker, A., Matrix groups. An introduction to Lie group theory. Springer-Verlag, London, 2002. http://dx.doi.org/10.1007/978-1-4471-0183-3
Google Scholar
[2]
Fine, B. and M. Newman, The normal subgroup structure of the Picard group.
Trans. Amer. Math. Soc.
302(1987), no. 2, 769–786. http://dx.doi.org/10.1090/S0002-9947-1987-0891646-3
Google Scholar
[3]
Goldstein, H., Classical mechanics. 2nd edition. Addison-Wesley, Reading, MA, 1980. Google Scholar
[4]
Jensen, G. and C. Pommerenke, Discrete space-time and Lorentz transformations.
Canad Math. Bull.
59(2016), no. 2, 123–135. http://dx.doi.org/10.41 53/CMB-2O1 5-066-4
Google Scholar
[5]
LorenteandP, M.. Kramer, Representations of the discrete inhomogeneous Lorentz group and Dirac wave equation on the lattice.
J. Phys. A
32(1999), 2481–2497. http://dx.doi.org/1 0.1088/0305-4470/32/12/01 9
Google Scholar
[6]
Louck, J. D., A new parametrization and all integral realizations of the Lorentz group.
J. Math. Phys.
43(2002), no. 10, 5108–5134. http://dx.doi.org/10.1063/1.1505124
Google Scholar
[7]
Penrose, R. and W. Rindler, Spinors and space-time. Volume I. Cambridge University Press, Cambridge, 1984. http://dx.doi.org/10.1 01 7/CBO9780511 564048
Google Scholar
[8]
Schild, A., Discrete space-time and integral Lorentz transformations.
Canad. J. Math.
1(1949), 29–47. http://dx.doi.org/! 0.41 53/CJM-1 949-003-4
Google Scholar

