Article contents
On the Structure of Cuntz Semigroups in (Possibly) Nonunital C*-algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
We examine the ranks of operators in semi-finite 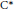 ${{C}^{*}}$ -algebras as measured by their densely defined lower semicontinuous traces. We first prove that a unital simple
${{C}^{*}}$ -algebras as measured by their densely defined lower semicontinuous traces. We first prove that a unital simple 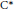 ${{C}^{*}}$ -algebra whose extreme tracial boundary is nonempty and finite contains positive operators of every possible rank, independent of the property of strict comparison. We then turn to nonunital simple algebras and establish criteria that imply that the Cuntz semigroup is recovered functorially from the Murray–von Neumann semigroup and the space of densely defined lower semicontinuous traces. Finally, we prove that these criteria are satisfied by not-necessarily-unital approximately subhomogeneous algebras of slow dimension growth. Combined with results of the first author, this shows that slow dimension growth coincides with
${{C}^{*}}$ -algebra whose extreme tracial boundary is nonempty and finite contains positive operators of every possible rank, independent of the property of strict comparison. We then turn to nonunital simple algebras and establish criteria that imply that the Cuntz semigroup is recovered functorially from the Murray–von Neumann semigroup and the space of densely defined lower semicontinuous traces. Finally, we prove that these criteria are satisfied by not-necessarily-unital approximately subhomogeneous algebras of slow dimension growth. Combined with results of the first author, this shows that slow dimension growth coincides with  $Z$ -stability for approximately subhomogeneous algebras.
$Z$ -stability for approximately subhomogeneous algebras.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 9
- Cited by

