Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Murty, Ram
and
Zaharescu, Alexandru
2002.
Explicit formulas for the pair correlation of zeros of functions in the Selberg class.
Forum Mathematicum,
Vol. 14,
Issue. 1,
Akbary, Amir
and
Shahabi, Shahab
2005.
On Non-Vanishing of Convolution of Dirichlet Series.
Canadian Mathematical Bulletin,
Vol. 48,
Issue. 3,
p.
321.
Omar, Sami
and
Mazhouda, Kamel
2007.
Le critère de Li et l'hypothèse de Riemann pour la classe de Selberg.
Journal of Number Theory,
Vol. 125,
Issue. 1,
p.
50.
Smajlović, Lejla
2010.
On Li's criterion for the Riemann hypothesis for the Selberg class.
Journal of Number Theory,
Vol. 130,
Issue. 4,
p.
828.
Bui, H. M.
Keating, J. P.
and
Smith, D. J.
2016.
On the variance of sums of arithmetic functions over primes in short intervals and pair correlation forL-functions in the Selberg class.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
161.

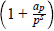 in
in 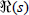 > 1, and which are regular in
> 1, and which are regular in 