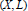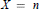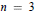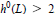Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fukuma, Yoshiaki
2000.
On complexn-folds polarized by an ample line bundle L with ..
Communications in Algebra,
Vol. 28,
Issue. 12,
p.
5769.
Fukuma, Yoshiaki
2004.
On the Sectional Geometric Genus of Quasi-Polarized Varieties. I.
Communications in Algebra,
Vol. 32,
Issue. 3,
p.
1069.
Fukuma, Yoshiaki
2004.
On the second sectional geometric genus of quasi-polarized manifolds.
advg,
Vol. 4,
Issue. 2,
p.
215.
FUKUMA, YOSHIAKI
2006.
ON A CONJECTURE OF BELTRAMETTI–SOMMESE FOR POLARIZED 3-FOLDS.
International Journal of Mathematics,
Vol. 17,
Issue. 07,
p.
761.
Fukuma, Yoshiaki
2007.
On the dimension of global sections of adjoint bundles for polarized 3-folds and 4-folds.
Journal of Pure and Applied Algebra,
Vol. 211,
Issue. 3,
p.
609.
Fukuma, Yoshiaki
2011.
Effective non-vanishing of global sections of multiple adjoint bundles for polarized 3-folds.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 2,
p.
168.
Fukuma, Yoshiaki
2016.
On Polarized 3-Folds (X,L) Such That <lowercase > h< /lowercase >0(L) = 2 and the Sectional Genus of (X,L) is Equal to the Irregularity ofX.
Communications in Algebra,
Vol. 44,
Issue. 4,
p.
1728.
FUKUMA, Yoshiaki
2017.
ON THE DIMENSION OF <i>H</i><sup>0</sup><i>(K</i><i><sub>X </sub></i>+ <i>mL) </i>OF POLARIZED <i>n</i>-FOLDS (<i>X</i>,<i> L</i>) WITH <i>m </i>≥ <i>n </i>.
Kyushu Journal of Mathematics,
Vol. 71,
Issue. 1,
p.
115.