Article contents
On the Moduli Space of a Spherical Polygonal Linkage
Published online by Cambridge University Press: 20 November 2018
Abstract
We give a “wall-crossing” formula for computing the topology of the moduli space of a closed 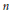 $n$ -gon linkage on
$n$ -gon linkage on 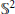 ${{\mathbb{S}}^{2}}$ . We do this by determining the Morse theory of the function
${{\mathbb{S}}^{2}}$ . We do this by determining the Morse theory of the function 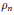 ${{\rho }_{n}}$ on the moduli space of
${{\rho }_{n}}$ on the moduli space of 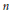 $n$ -gon linkages which is given by the length of the last side—the length of the last side is allowed to vary, the first
$n$ -gon linkages which is given by the length of the last side—the length of the last side is allowed to vary, the first 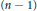 $\left( n\,-\,1 \right)$ side-lengths are fixed. We obtain a Morse function on the
$\left( n\,-\,1 \right)$ side-lengths are fixed. We obtain a Morse function on the 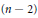 $\left( n\,-\,2 \right)$ -torus with level sets moduli spaces of
$\left( n\,-\,2 \right)$ -torus with level sets moduli spaces of 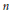 $n$ -gon linkages. The critical points of
$n$ -gon linkages. The critical points of 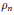 ${{\rho }_{n}}$ are the linkages which are contained in a great circle. We give a formula for the signature of the Hessian of
${{\rho }_{n}}$ are the linkages which are contained in a great circle. We give a formula for the signature of the Hessian of 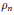 ${{\rho }_{n}}$ at such a linkage in terms of the number of back-tracks and the winding number. We use our formula to determine the moduli spaces of all regular pentagonal spherical linkages.
${{\rho }_{n}}$ at such a linkage in terms of the number of back-tracks and the winding number. We use our formula to determine the moduli spaces of all regular pentagonal spherical linkages.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
- 14
- Cited by

