Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Broeksteeg, Raymond
1994.
A concept of variety for regular biordered sets.
Semigroup Forum,
Vol. 49,
Issue. 1,
p.
335.
Broeksteeg, Raymond E.
1995.
E-solid regular semigroups and solid binary algebras.
Bulletin of the Australian Mathematical Society,
Vol. 51,
Issue. 1,
p.
171.
Szendrei, Mária B.
1996.
The bifree regularE-solid semigroups.
Semigroup Forum,
Vol. 52,
Issue. 1,
p.
61.
Auinger, K.
and
Hall, T.E.
1996.
Concepts of congruence, morphic image and substructure for biordered sets†.
Communications in Algebra,
Vol. 24,
Issue. 12,
p.
3933.
Pastijn, Francis J.
and
Oliveira, Luís A.
2008.
Rees Matrix Covers and the Translational Hull of a Locally Inverse Semigroup.
Communications in Algebra,
Vol. 36,
Issue. 9,
p.
3230.
Auinger, K.
and
Oliveira, L.
2013.
On the variety of strict pseudosemilattices.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 50,
Issue. 2,
p.
207.
Oliveira, Luís
2015.
A family of varieties of pseudosemilattices.
Semigroup Forum,
Vol. 91,
Issue. 1,
p.
71.
Oliveira, Luís
2018.
The free idempotent generated locally inverse semigroup.
Semigroup Forum,
Vol. 96,
Issue. 3,
p.
452.

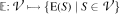 which assigns to each existence variety
which assigns to each existence variety 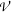 of locally inverse semigroups the class of all pseudosemilattices of idempotents of members of
of locally inverse semigroups the class of all pseudosemilattices of idempotents of members of 