No CrossRef data available.
Article contents
On the Injective and Projective Limit of Complexes
Published online by Cambridge University Press: 20 November 2018
Extract
Let R be a commutative ring with unit. Let (Aα, φ βα) (α ≤ β) (resp. (Bα, ψαβ) (α ≤ β)) be an infective (resp. projective) system of R-algebras indexed by a directed set I; let ((Xα, dα), fβα) (α ≤ β) (resp. ((Yα, δα), gαβ) (α≤β)) be an injective (resp. projective) system of complexes, indexed by the same set I, such that for each αϵI, (Xα, dα) (resp. (Yα, δα)) is a complex over Aα (resp. over Bα). The purpose of this paper is to show that the covariant functor 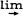 from the category of all such injective systems of complexes and complex homomorphisms over the R-algebra
from the category of all such injective systems of complexes and complex homomorphisms over the R-algebra 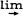 Aα is such that it associates with an injective system ((Uα, dα), hβα) of universal complexes a universal complex over
Aα is such that it associates with an injective system ((Uα, dα), hβα) of universal complexes a universal complex over 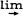 Aα whereas the same is not true of the covariant functor
Aα whereas the same is not true of the covariant functor 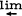 the category of all such projective systems of complexes and their maps.
the category of all such projective systems of complexes and their maps.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1965
Footnotes
The author wishes to express her thanks to Professor B. Banaschewski for his guidance during the preparation of this work.

