Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Győry, K.
Hajdu, L.
and
Saradha, N.
2005.
Correction to: On the Diophantine Equation n(n + d) · · · (n + (k – 1)d) = byl.
Canadian Mathematical Bulletin,
Vol. 48,
Issue. 4,
p.
636.
Győry, Kálmán
2006.
More Sets, Graphs and Numbers.
Vol. 15,
Issue. ,
p.
143.
Győry, K.
Hajdu, L.
and
Pintér, Á.
2009.
Perfect powers from products of consecutive terms in arithmetic progression.
Compositio Mathematica,
Vol. 145,
Issue. 4,
p.
845.
Yang, Shichun
Togbé, Alain
and
He, Bo
2011.
Diophantine equations with products of consecutive values of a quadratic polynomial.
Journal of Number Theory,
Vol. 131,
Issue. 10,
p.
1840.
Hajdu, L.
and
Kovács, T.
2011.
Almost fifth powers in arithmetic progression.
Journal of Number Theory,
Vol. 131,
Issue. 10,
p.
1912.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Győry, Kálmán
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
311.
Tengely, Szabolcs
and
Varga, Nóra
2015.
Rational function variant of a problem of Erdös and Graham.
Glasnik Matematicki,
Vol. 50,
Issue. 1,
p.
65.
Bennett, Michael A.
and
Siksek, Samir
2016.
Rational points on Erdős–Selfridge superelliptic curves.
Compositio Mathematica,
Vol. 152,
Issue. 11,
p.
2249.
Tengely, Szabolcs
2016.
On a problem of Erdős and Graham.
Periodica Mathematica Hungarica,
Vol. 72,
Issue. 1,
p.
23.
Tengely, Sz.
and
Ulas, M.
2016.
On products of disjoint blocks of arithmetic progressions and related equations.
Journal of Number Theory,
Vol. 165,
Issue. ,
p.
67.
Zhang, Y.
2018.
On products of consecutive arithmetic progressions. II.
Acta Mathematica Hungarica,
Vol. 156,
Issue. 1,
p.
240.
Munshi, Ritabrata
2019.
Analytic number theory in India during 2001–2010.
Indian Journal of Pure and Applied Mathematics,
Vol. 50,
Issue. 3,
p.
719.
Klurman, Oleksiy
and
Munsch, Marc
2020.
Polynomial products modulo primes and applications.
Monatshefte für Mathematik,
Vol. 191,
Issue. 3,
p.
577.
Hajdu, L.
and
Papp, Á.
2020.
Polynomial values of products of terms from an arithmetic progression.
Monatshefte für Mathematik,
Vol. 193,
Issue. 3,
p.
637.
Zhang, Y.
2021.
On products of consecutive arithmetic progressions. III.
Acta Mathematica Hungarica,
Vol. 163,
Issue. 2,
p.
407.
Natarajan, Saradha
2025.
Perfect Powers—An Ode to Erdős.
p.
145.
Natarajan, Saradha
2025.
Perfect Powers—An Ode to Erdős.
p.
163.
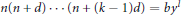 $n(n\,+\,d)\,\cdots \,(n\,+\,(k\,-\,1)d)\,=\,b{{y}^{l}}$
$n(n\,+\,d)\,\cdots \,(n\,+\,(k\,-\,1)d)\,=\,b{{y}^{l}}$  $n,\,y$ when
$n,\,y$ when 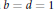 $b\,=\,d\,=\,1$ . We show that there are only finitely many solutions in
$b\,=\,d\,=\,1$ . We show that there are only finitely many solutions in 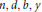 $n,\,d,\,b,\,y$ when
$n,\,d,\,b,\,y$ when  $k\,\ge \,3,\,l\,\ge \,2$ are fixed and
$k\,\ge \,3,\,l\,\ge \,2$ are fixed and 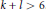 $k\,+\,l\,>\,6$ .
$k\,+\,l\,>\,6$ .
