Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Müller, Bruno J.
and
Rizvi, S.Tariq
1983.
On injective and quasi-continuous modules.
Journal of Pure and Applied Algebra,
Vol. 28,
Issue. 2,
p.
197.
Tariq Rizvi, S.
1988.
Commutative rings for which every continuous module is quasi-injective.
Archiv der Mathematik,
Vol. 50,
Issue. 5,
p.
435.
Osofsky, Barbara L
and
Smith, Patrick F
1991.
Cyclic modules whose quotients have all complement submodules direct summands.
Journal of Algebra,
Vol. 139,
Issue. 2,
p.
342.
Smith, Patrick F.
1997.
Advances in Ring Theory.
p.
305.
López-Permouth, S.R.
Oshiro, Kiyoichi
and
Rizvi, Tariq S.
1998.
On the relative (quasi-) continuity of modules.
Communications in Algebra,
Vol. 26,
Issue. 11,
p.
3497.
Tuganbaev, A. A.
1999.
Skew-injective modules.
Journal of Mathematical Sciences,
Vol. 95,
Issue. 4,
p.
2328.
Dauns, John
and
Zhou, Yiqiang
2005.
Type Submodules and Direct Sum Decompositions of Modules.
Rocky Mountain Journal of Mathematics,
Vol. 35,
Issue. 1,
Birkenmeier, Gary F.
Park, Jae Keol
and
Rizvi, S. Tariq
2013.
Extensions of Rings and Modules.
p.
19.

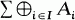 of indecomposable summands
of indecomposable summands 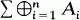 of indecomposable modules
of indecomposable modules 